Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T18:47:31.717Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow instabilities in the wake of a circular cylinder with parallel dual splitter plates attached

Published online by Cambridge University Press:  04 July 2019

Rui Wang ,
Yan Bao ,
Dai Zhou ,
Hongbo Zhu Open the ORCID record for Hongbo Zhu [Opens in a new window] ,
Huan Ping ,
Zhaolong Han ,
Douglas Serson Open the ORCID record for Douglas Serson [Opens in a new window]  and
Hui Xu
Rui Wang
Affiliation:
School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China
Yan Bao*
Affiliation:
School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China Key Laboratory of Hydrodynamics of Ministry of Education, Shanghai, 200240, China
Dai Zhou*
Affiliation:
School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China Key Laboratory of Hydrodynamics of Ministry of Education, Shanghai, 200240, China State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai, 200240, China
Hongbo Zhu
Affiliation:
School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China
Huan Ping
Affiliation:
School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China
Zhaolong Han
Affiliation:
School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China Key Laboratory of Hydrodynamics of Ministry of Education, Shanghai, 200240, China
Douglas Serson
Affiliation:
Núcleo de Dinâmica e Fluidos (NDF), Escola Politécnica, Universidade de São Paulo, Av. Prof. Mello Moraes, 2231, São Paulo, 05508-030, Brazil
Hui Xu
Affiliation:
School of Aeronautics and Astronautics, Shanghai Jiao Tong University, Shanghai, 200240, China
*
†Email addresses for correspondence: ybao@sjtu.edu.cn, zhoudai@sjtu.edu.cn
†Email addresses for correspondence: ybao@sjtu.edu.cn, zhoudai@sjtu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

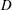In this paper, instabilities in the flow over a circular cylinder of diameter $D$ with dual splitter plates attached to its rear surface are numerically investigated using the spectral element method. The key parameters are the splitter plate length 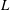$L$, the attachment angle $\unicode[STIX]{x1D6FC}$ and the Reynolds number 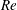$Re$. The presence of the plates was found to significantly modify the flow topology, leading to substantial changes in both the primary and secondary instabilities. The results showed that the three instability modes present in the bare circular cylinder wake still exist in the wake of the present configurations and that, in general, the occurrences of modes A and B are delayed, while the onset of mode QP is earlier in the presence of the splitter plates. Furthermore, two new synchronous modes, referred to as mode A$^{\prime }$ and mode B$^{\prime }$, are found to develop in the wake. Mode A$^{\prime }$ is similar to mode A but with a quite long critical wavelength. Mode B$^{\prime }$ shares the same spatio-temporal symmetries as mode B but has a distinct spatial structure. With the exception of the case of $L/D=0.25$, mode A$^{\prime }$ persists for all configurations investigated here and always precedes the transition through mode A. 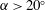The onset of mode B$^{\prime }$ occurs for $\unicode[STIX]{x1D6FC}>20^{\circ }$ with $L/D=1.0$ and for $L/D>0.5$ with $\unicode[STIX]{x1D6FC}=60^{\circ }$. The characteristics of all the transition modes are analysed, and their similarities and differences are discussed in detail in comparison with the existing modes. In addition, the physical mechanism responsible for the instability mode B$^{\prime }$ is proposed. The weakly nonlinear feature of mode B$^{\prime }$, as well as that of mode A$^{\prime }$, is assessed by employing the Landau model. Finally, selected three-dimensional simulations are performed to confirm the existence of these two new modes and to investigate the nonlinear evolution of the three-dimensional modes.

JFM classification

Flow Control: Instability control Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 299 - 338
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdi, R., Rezazadeh, N. & Abdi, M. 2017 Reduction of fluid forces and vortex shedding frequency of a circular cylinder using rigid splitter plates. Eur. J. Comput. Mech. 26 (3), 225–244.Google Scholar
Åkervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18 (6), 068102.Google Scholar
Assi, G. R. S., Bearman, P. W. & Kitney, N. 2009 Low drag solutions for suppressing vortex-induced vibration of circular cylinders. J. Fluids Struct. 25 (4), 666–675.Google Scholar
Assi, G. R. S., Bearman, P. W., Kitney, N. & Tognarelli, M. A. 2010 Suppression of wake-induced vibration of tandem cylinders with free-to-rotate control plates. J. Fluids Struct. 26 (7-8), 1045–1057.Google Scholar
Assi, G. R. S., Franco, G. S. & Vestri, M. S. 2014 Investigation on the stability of parallel and oblique plates as suppressors of vortex-induced vibration of a circular cylinder. J. Offshore Mech. Arctic Engng. 136 (3), 031802.Google Scholar
Assi, G. R. S., Rodrigues, J. R. H. & Freire, C. M. 2012 The effect of plate length on the behaviour of free-to-rotate viv suppressors with parallel plates. In ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, pp. 791–798. ASME.Google Scholar
Baarholm, R., Skaugset, K., Lie, H. & Braaten, H. 2015 Experimental studies of hydrodynamic properties and screening of riser fairing concepts for deep water applications. In ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, p. V002T08A054. ASME.Google Scholar
Bao, Y. & Tao, J. 2013 The passive control of wake flow behind a circular cylinder by parallel dual plates. J. Fluids Struct. 37, 201–219.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Blackburn, H. M., Marques, F. & Lopez, J. M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J. Fluid Mech. 522, 395–411.Google Scholar
Cantwell, C. D., Moxey, D., Comerford, A., Bolis, A., Rocco, G., Mengaldo, G., De Grazia, D., Yakovlev, S., Lombard, J. E., Ekelschot, D. et al. 2015 Nektar++: an open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219.Google Scholar
Carmo, B. S., Meneghini, J. R. & Sherwin, S. J. 2010 Secondary instabilities in the flow around two circular cylinders in tandem. J. Fluid Mech. 644, 395–431.Google Scholar
Carmo, B. S., Sherwin, S. J., Bearman, P. W. & Willden, R. H. J. 2008 Wake transition in the flow around two circular cylinders in staggered arrangements. J. Fluid Mech. 597, 1–29.Google Scholar
Chandrmohan, A. A.2009 Effect of base cavities on the drag and wake of a two-dimensional bluff body. PhD thesis, King Fahd University of Petroleum and Minerals.Google Scholar
Choi, H., Jeon, W. P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40 (1), 113–139.Google Scholar
Dušek, J., Le Gal, P. & Fraunié, P. 1994 A numerical and theoretical study of the first Hopf bifurcation in a cylinder wake. J. Fluid Mech. 264, 59–80.Google Scholar
Grimminger, G.1945 The effect of rigid guide vanes on the vibration and drag of a towed circular cylinder. Tech. Rep. 504. David Taylor Model Basin, Washinton DC, USA.Google Scholar
Guermond, J. L. & Shen, J. 2003 Velocity-correction projection methods for incompressible flows. SIAM J. Numer. Anal. 41 (1), 112–134.Google Scholar
Henderson, R. D. 1995 Details of the drag curve near the onset of vortex shedding. Phys. Fluids 7 (9), 2102–2104.Google Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.Google Scholar
Henderson, R. D. & Barkley, D. 1996 Secondary instability in the wake of a circular cylinder. Phys. Fluids 8 (6), 1683–1685.Google Scholar
Jiménez-González, J. I., Sanmiguel-Rojas, E., Sevilla, A. & Martínez-Bazán, C. 2013 Laminar flow past a spinning bullet-shaped body at moderate angular velocities. J. Fluids Struct. 43, 200–219.Google Scholar
Karniadakis, G. E. 1990 Spectral element-Fourier methods for incompressible turbulent flows. Comput. Meth. Appl. Mech. Engng 80 (1-3), 367–380.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier-Stokes equations. J. Comput. Phys. 97 (2), 414–443.Google Scholar
Karniadakis, G. E. & Sherwin, S. J. 2013 Spectral/hp Element Methods for Computational Fluid Dynamics. Oxford University Press.Google Scholar
Kevlahan, N. K. R. 2007 Three-dimensional Floquet stability analysis of the wake in cylinder arrays. J. Fluid Mech. 592, 79–88.Google Scholar
Kruiswyk, R. W. & Dutton, J. C. 1990 Effects of a base cavity on subsonic near-wake flow. AIAA J. 28 (11), 1885–1893.Google Scholar
Kumar, B. & Mittal, S. 2006 Prediction of the critical Reynolds number for flow past a circular cylinder. Comput. Meth. Appl. Mech. Engng 195 (44-47), 6046–6058.Google Scholar
Lagnado, R. R., Phan-Thien, N. & Leal, L. G. 1984 The stability of two-dimensional linear flows. Phys. Fluids 27 (5), 1094–1101.Google Scholar
Law, Y. Z. & Jaiman, R. K. 2017 Wake stabilization mechanism of low-drag suppression devices for vortex-induced vibration. J. Fluids Struct. 70, 428–449.Google Scholar
Leontini, J. S., Lo Jacono, D. & Thompson, M. C. 2015 Stability analysis of the elliptic cylinder wake. J. Fluid Mech. 763, 302–321.Google Scholar
Mamun, C. K. & Tuckerman, L. S. 1995 Asymmetry and Hopf bifurcation in spherical Couette flow. Phys. Fluids 7 (1), 80–91.Google Scholar
Marques, F., Lopez, J. M. & Blackburn, H. M. 2004 Bifurcations in systems with Z2 spatio-temporal and O(2) spatial symmetry. Phys. D 189 (3), 247–276.Google Scholar
Molezzi, M. J. & Dutton, J. C. 1995 Study of subsonic base cavity flowfield structure using particle image velocimetry. AIAA J. 33 (2), 201–209.Google Scholar
Ng, Z. Y., Vo, T. & Sheard, G. J. 2018 Stability of the wakes of cylinders with triangular cross-sections. J. Fluid Mech. 844, 721–745.Google Scholar
Park, D. & Yang, K. 2016 Flow instabilities in the wake of a rounded square cylinder. J. Fluid Mech. 793, 915–932.Google Scholar
Pontaza, J. P., Kotikanyadanam, M., Moeleker, P., Menon, R. G. & Bhat, S. 2012 Fairing evaluation based on numerical simulation. In ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, pp. 897–905. ASME.Google Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard-von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.Google Scholar
Qu, L., Norberg, C., Davidson, L., Peng, S. & Wang, F. 2013 Quantitative numerical analysis of flow past a circular cylinder at Reynolds number between 50 and 200. J. Fluids Struct. 39, 347–370.Google Scholar
Rao, A., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2017 Three-dimensionality of elliptical cylinder wakes at low angles of incidence. J. Fluid Mech. 825, 245–283.Google Scholar
Rashidi, S., Hayatdavoodi, M. & Esfahani, J. A. 2016 Vortex shedding suppression and wake control: A review. Ocean Engng 126, 57–80.Google Scholar
Ryan, K., Thompson, M. C. & Hourigan, K. 2005 Three-dimensional transition in the wake of bluff elongated cylinders. J. Fluid Mech. 538, 1–29.Google Scholar
Schaudt, K. J., Wajnikonis, C., Spencer, D., Xu, J., Leverette, S. & Masters, R. 2008 Benchmarking of viv suppression systems. In ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering, pp. 33–42. ASME.Google Scholar
Serson, D., Meneghini, J. R., Carmo, B. S., Volpe, E. V. & Gioria, R. S. 2014 Wake transition in the flow around a circular cylinder with a splitter plate. J. Fluid Mech. 755, 582–602.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004 From spheres to circular cylinders: non-axisymmetric transitions in the flow past rings. J. Fluid Mech. 506, 45–78.Google Scholar
Taggart, S. & Tognarelli, M. A. 2008 Offshore drilling riser VIV suppression devices: What’s available to operators? In ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering, pp. 527–537. ASME.Google Scholar
Taherian, G., Nili-Ahmadabadi, M., Karimi, M. H. & Tavakoli, M. R. 2017 Flow visualization over a thick blunt trailing-edge airfoil with base cavity at low Reynolds numbers using PIV technique. J. Vis. 20 (4), 695–710.Google Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15 (3-4), 607–616.Google Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31 (11), 3165–3168.Google Scholar
Williamson, C. H. K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar
Xie, F., Yu, Y., Constantinides, Y., Triantafyllou, M. S. & Karniadakis, G. E. 2015 U-shaped fairings suppress vortex-induced vibrations for cylinders in cross-flow. J. Fluid Mech. 782, 300–332.Google Scholar
Xu, H., Cantwell, C. D., Monteserin, C., Eskilsson, C., Engsig-Karup, A. P. & Sherwin, S. J. 2018 Spectral/hp element methods: Recent developments, applications, and perspectives. J. Hydrodyn. 30 (1), 1–22.Google Scholar
Yang, D., Pettersen, B., Andersson, H. I. & Narasimhamurthy, V. D. 2013 Floquet stability analysis of the wake of an inclined flat plate. Phys. Fluids 25 (9), 094103.Google Scholar
Yu, Y., Xie, F., Yan, H., Constantinides, Y., Oakley, O. & Karniadakis, G. E. 2015 Suppression of vortex-induced vibrations by fairings: a numerical study. J. Fluids Struct. 54, 679–700.Google Scholar