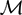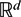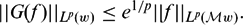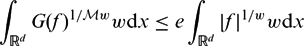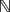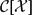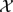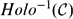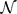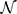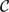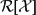Research Article
THE GROUP OF AUTOMORPHISMS OF THE LIE ALGEBRA OF DERIVATIONS OF A FIELD OF RATIONAL FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 513-524
-
- Article
-
- You have access
- Export citation
HOMOTOPY THEORY OF MODULES AND ADAMS COCOMPLETION
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 525-532
-
- Article
-
- You have access
- Export citation
SHARP WEIGHTED BOUNDS FOR GEOMETRIC MAXIMAL OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 533-547
-
- Article
-
- You have access
- Export citation
THE STRUCTURE OF BALANCED BIG COHEN–MACAULAY MODULES OVER COHEN–MACAULAY RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 549-561
-
- Article
-
- You have access
- Export citation
NON-AFFINE HOPF ALGEBRA DOMAINS OF GELFAND–KIRILLOV DIMENSION TWO
-
- Published online by Cambridge University Press:
- 20 March 2017, pp. 563-593
-
- Article
-
- You have access
- Export citation
DEGREE CONES AND MONOMIAL BASES OF LIE ALGEBRAS AND QUANTUM GROUPS
-
- Published online by Cambridge University Press:
- 20 March 2017, pp. 595-621
-
- Article
-
- You have access
- Export citation
SOME NEW EXAMPLES OF SMASH-NILPOTENT ALGEBRAIC CYCLES
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 623-634
-
- Article
-
- You have access
- Export citation
PERTURBATIONS FROM INDEFINITE SYMMETRIC ELLIPTIC BOUNDARY VALUE PROBLEMS
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2017, pp. 635-648
-
- Article
-
- You have access
- Export citation
ON SERRE MICROFIBRATIONS AND A LEMMA OF M. WEISS
-
- Published online by Cambridge University Press:
- 20 March 2017, pp. 649-657
-
- Article
-
- You have access
- Export citation
PERTURBATION OF BANACH SPACE OPERATORS WITH A COMPLEMENTED RANGE
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2017, pp. 659-671
-
- Article
-
- You have access
- Export citation
THE IDEMPOTENT-GENERATED SUBSEMIGROUP OF THE KAUFFMAN MONOID
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2017, pp. 673-683
-
- Article
-
- You have access
- Export citation
GORENSTEIN MODULES AND GORENSTEIN MODEL STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2017, pp. 685-703
-
- Article
-
- You have access
- Export citation
ON THE STANLEY DEPTH AND SIZE OF MONOMIAL IDEALS
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2017, pp. 705-715
-
- Article
-
- You have access
- Export citation
SOME SPHERE THEOREMS FOR SUBMANIFOLDS WITH POSITIVE BIORTHOGONAL CURVATURE
-
- Published online by Cambridge University Press:
- 07 February 2017, pp. 717-728
-
- Article
-
- You have access
- Export citation
RELATIVE HILBERT CO-EFFICIENTS
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2017, pp. 729-741
-
- Article
-
- You have access
- Export citation
EIGENVALUES OF GEOMETRIC OPERATORS RELATED TO THE WITTEN LAPLACIAN UNDER THE RICCI FLOW
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2017, pp. 743-751
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
GMJ volume 59 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
GMJ volume 59 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation