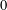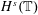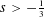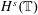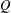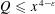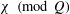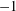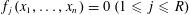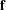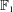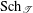Theoretical Computer Science
Research Article
COMPLEXITY OF SHORT GENERATING FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2018, e1
-
- Article
-
- You have access
- Open access
- Export citation
Discrete Mathematics
Research Article
TILING DIRECTED GRAPHS WITH TOURNAMENTS
-
- Published online by Cambridge University Press:
- 14 February 2018, e2
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
Research Article
VANISHING IN STABLE MOTIVIC HOMOTOPY SHEAVES
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2018, e3
-
- Article
-
- You have access
- Open access
- Export citation
Topology
Research Article
HILBERT STRATIFOLDS AND A QUILLEN TYPE GEOMETRIC DESCRIPTION OF COHOMOLOGY FOR HILBERT MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2018, e4
-
- Article
-
- You have access
- Open access
- Export citation
Differential Equations
Research Article
GLOBAL WELL-POSEDNESS OF THE PERIODIC CUBIC FOURTH ORDER NLS IN NEGATIVE SOBOLEV SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2018, e5
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Research Article
LOCAL SYSTEMS ON COMPLEMENTS OF ARRANGEMENTS OF SMOOTH, COMPLEX ALGEBRAIC HYPERSURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2018, e6
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
ANY CYCLIC QUADRILATERAL CAN BE INSCRIBED IN ANY CLOSED CONVEX SMOOTH CURVE
- Part of:
-
- Published online by Cambridge University Press:
- 31 May 2018, e7
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
RAPOPORT–ZINK SPACES OF HODGE TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2018, e8
-
- Article
-
- You have access
- Open access
- Export citation
Differential Equations
Research Article
CONDITIONAL LARGE INITIAL DATA SCATTERING RESULTS FOR THE DIRAC–KLEIN–GORDON SYSTEM
- Part of:
-
- Published online by Cambridge University Press:
- 21 June 2018, e9
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
ON BINARY CORRELATIONS OF MULTIPLICATIVE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 28 June 2018, e10
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
Research Article
MODULAR DECOMPOSITION NUMBERS OF CYCLOTOMIC HECKE AND DIAGRAMMATIC CHEREDNIK ALGEBRAS: A PATH THEORETIC APPROACH
- Part of:
-
- Published online by Cambridge University Press:
- 03 July 2018, e11
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
SINGULARITIES OF THE BIEXTENSION METRIC FOR FAMILIES OF ABELIAN VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 23 July 2018, e12
-
- Article
-
- You have access
- Open access
- Export citation
UNLIKELY INTERSECTIONS IN FINITE CHARACTERISTIC
-
- Published online by Cambridge University Press:
- 09 August 2018, e13
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
POINTWISE CONVERGENCE OF SCHRÖDINGER SOLUTIONS AND MULTILINEAR REFINED STRICHARTZ ESTIMATES
- Part of:
-
- Published online by Cambridge University Press:
- 13 August 2018, e14
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
Research Article
WHEN DOES THE BOMBIERI–VINOGRADOV THEOREM HOLD FOR A GIVEN MULTIPLICATIVE FUNCTION?
- Part of:
-
- Published online by Cambridge University Press:
- 24 August 2018, e15
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
RAPOPORT–ZINK UNIFORMIZATION OF HODGE-TYPE SHIMURA VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 03 September 2018, e16
-
- Article
-
- You have access
- Open access
- Export citation
Discrete Mathematics
Research Article
COLORING CURVES ON SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2018, e17
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
COMPACTIFICATIONS OF SUBSCHEMES OF INTEGRAL MODELS OF SHIMURA VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 24 September 2018, e18
-
- Article
-
- You have access
- Open access
- Export citation
PRIME SOLUTIONS TO POLYNOMIAL EQUATIONS IN MANY VARIABLES AND DIFFERING DEGREES
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2018, e19
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Research Article
THE GEOMETRY OF BLUEPRINTS PART II: TITS–WEYL MODELS OF ALGEBRAIC GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 23 October 2018, e20
-
- Article
-
- You have access
- Open access
- Export citation