Article contents
SINGULARITIES OF THE BIEXTENSION METRIC FOR FAMILIES OF ABELIAN VARIETIES
Published online by Cambridge University Press: 23 July 2018
Abstract
In this paper we study the singularities of the invariant metric of the Poincaré bundle over a family of abelian varieties and their duals over a base of arbitrary dimension. As an application of this study we prove the effectiveness of the height jump divisors for families of pointed abelian varieties. The effectiveness of the height jump divisor was conjectured by Hain in the more general case of variations of polarized Hodge structures of weight
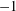 $-1$
.
$-1$
.
MSC classification
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2018
References
- 6
- Cited by





