Article contents
PRIME SOLUTIONS TO POLYNOMIAL EQUATIONS IN MANY VARIABLES AND DIFFERING DEGREES
Published online by Cambridge University Press: 18 October 2018
Abstract
Let 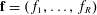 $\mathbf{f}=(f_{1},\ldots ,f_{R})$ be a system of polynomials with integer coefficients in which the degrees need not all be the same. We provide sufficient conditions for which the system of equations
$\mathbf{f}=(f_{1},\ldots ,f_{R})$ be a system of polynomials with integer coefficients in which the degrees need not all be the same. We provide sufficient conditions for which the system of equations 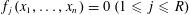 $f_{j}(x_{1},\ldots ,x_{n})=0~(1\leqslant j\leqslant R)$ satisfies a general local to global type statement, and has a solution where each coordinate is prime. In fact we obtain the asymptotic formula for number of such solutions, counted with a logarithmic weight, under these conditions. We prove the statement via the Hardy–Littlewood circle method. This is a generalization of the work of Cook and Magyar [‘Diophantine equations in the primes’, Invent. Math.198 (2014), 701–737], where they obtained the result when the polynomials of
$f_{j}(x_{1},\ldots ,x_{n})=0~(1\leqslant j\leqslant R)$ satisfies a general local to global type statement, and has a solution where each coordinate is prime. In fact we obtain the asymptotic formula for number of such solutions, counted with a logarithmic weight, under these conditions. We prove the statement via the Hardy–Littlewood circle method. This is a generalization of the work of Cook and Magyar [‘Diophantine equations in the primes’, Invent. Math.198 (2014), 701–737], where they obtained the result when the polynomials of 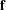 $\mathbf{f}$ all have the same degree. Hitherto, results of this type for systems of polynomial equations involving different degrees have been restricted to the diagonal case.
$\mathbf{f}$ all have the same degree. Hitherto, results of this type for systems of polynomial equations involving different degrees have been restricted to the diagonal case.
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives licence (http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits noncommercial re-use, distribution, and reproduction in any medium, provided the original work is unaltered and is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use or in order to create a derivative work.
- Copyright
- © The Author 2018
References
- 2
- Cited by


