Article contents
ANY CYCLIC QUADRILATERAL CAN BE INSCRIBED IN ANY CLOSED CONVEX SMOOTH CURVE
Published online by Cambridge University Press: 31 May 2018
Abstract
We prove that any cyclic quadrilateral can be inscribed in any closed convex 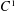 $C^{1}$-curve. The smoothness condition is not required if the quadrilateral is a rectangle.
$C^{1}$-curve. The smoothness condition is not required if the quadrilateral is a rectangle.
MSC classification
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2018
References
- 8
- Cited by



