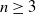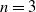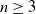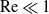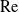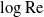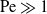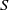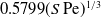Open access
Papers
Modelling of the fluid flow in a thin domain with injection through permeable boundary
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform propagation of chaos for a dollar exchange econophysics model
- Part of:
-
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Macroscopic limit of a Fokker-Planck model of swarming rigid bodies
- Part of:
-
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A finite-volume scheme for fractional diffusion on bounded domains
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large Péclet number forced convection from a circular wire in a uniform stream: hybrid approximations at small Reynolds numbers
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slow passage through the Busse balloon – predicting steps on the Eckhaus staircase
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Consensus-based optimisation with truncated noise
- Part of:
-
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Addendum
A data-driven kinetic model for opinion dynamics with social network contacts – ADDENDUM
-
- Published online by Cambridge University Press:
- 02 April 2024, p. 1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Papers
Measuring multidimensional heterogeneity in emergent social phenomena
-
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derivation and travelling wave analysis of phenotype-structured haptotaxis models of cancer invasion
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2024, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A data-driven kinetic model for opinion dynamics with social network contacts
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The turnpike property for mean-field optimal control problems
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From NeurODEs to AutoencODEs: A mean-field control framework for width-varying neural networks
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2024, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Network-based kinetic models: Emergence of a statistical description of the graph topology
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The dynamical analysis of a nonlocal predator–prey model with cannibalism
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2024, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global dynamics and spatiotemporal heterogeneity of a preytaxis model with prey-induced acceleration
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2024, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On degenerate reaction-diffusion epidemic models with mass action or standard incidence mechanism
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The fully parabolic multi-species chemotaxis system in
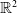 $\mathbb{R}^{2}$
$\mathbb{R}^{2}$
- Part of:
-
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Recurrent and chaotic outbreaks in SIR model
-
- Published online by Cambridge University Press:
- 18 January 2024, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Absolute concentration robustness and multistationarity in reaction networks: Conditions for coexistence
- Part of:
-
- Published online by Cambridge University Press:
- 02 January 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation