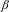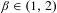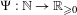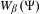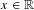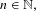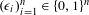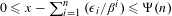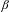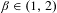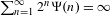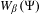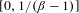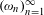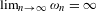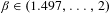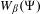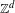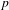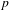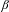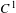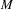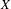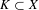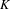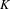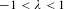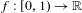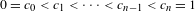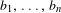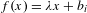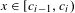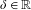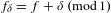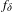Original Article
On some symmetric multidimensional continued fraction algorithms
-
- Published online by Cambridge University Press:
- 24 January 2017, pp. 1601-1626
-
- Article
- Export citation
Approximation properties of
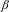 $\unicode[STIX]{x1D6FD}$-expansions II
$\unicode[STIX]{x1D6FD}$-expansions II
-
- Published online by Cambridge University Press:
- 14 February 2017, pp. 1627-1641
-
- Article
- Export citation
Fixed point theorems for metric spaces with a conical geodesic bicombing
-
- Published online by Cambridge University Press:
- 14 February 2017, pp. 1642-1657
-
- Article
- Export citation
The topological strong spatial mixing property and new conditions for pressure approximation
-
- Published online by Cambridge University Press:
- 04 May 2017, pp. 1658-1696
-
- Article
- Export citation
Asymptotic estimate for the counting problems corresponding to the dynamical system on some decorated graphs
-
- Published online by Cambridge University Press:
- 24 January 2017, pp. 1697-1708
-
- Article
- Export citation
Oscillating sequences, MMA and MMLS flows and Sarnak’s conjecture
-
- Published online by Cambridge University Press:
- 14 March 2017, pp. 1709-1744
-
- Article
- Export citation
On density of ergodic measures and generic points
-
- Published online by Cambridge University Press:
- 08 November 2016, pp. 1745-1767
-
- Article
- Export citation
Topologically irreducible representations of the Banach
 $\ast$-algebra associated with a dynamical system
$\ast$-algebra associated with a dynamical system
-
- Published online by Cambridge University Press:
- 24 January 2017, pp. 1768-1790
-
- Article
- Export citation
Fully essential dynamics for area-preserving surface homeomorphisms
-
- Published online by Cambridge University Press:
- 14 February 2017, pp. 1791-1836
-
- Article
- Export citation
Counting preimages
-
- Published online by Cambridge University Press:
- 24 January 2017, pp. 1837-1856
-
- Article
- Export citation
Necessary and sufficient conditions for stable synchronization in random dynamical systems
-
- Published online by Cambridge University Press:
- 24 January 2017, pp. 1857-1875
-
- Article
- Export citation
Topological dynamics of piecewise
 $\unicode[STIX]{x1D706}$-affine maps
$\unicode[STIX]{x1D706}$-affine maps
-
- Published online by Cambridge University Press:
- 10 November 2016, pp. 1876-1893
-
- Article
- Export citation
Topologically completely positive entropy and zero-dimensional topologically completely positive entropy
-
- Published online by Cambridge University Press:
- 14 March 2017, pp. 1894-1922
-
- Article
- Export citation
Traces on topological-graph algebras
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1923-1953
-
- Article
- Export citation
The error term in the prime orbit theorem for expanding semiflows
-
- Published online by Cambridge University Press:
- 24 January 2017, pp. 1954-2000
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 38 Issue 5 Cover and Front matter
-
- Published online by Cambridge University Press:
- 02 July 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 38 Issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 02 July 2018, pp. b1-b2
-
- Article
-
- You have access
- Export citation