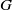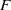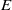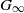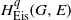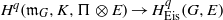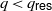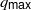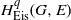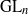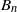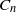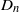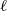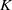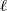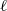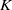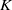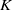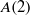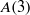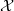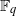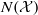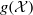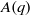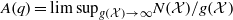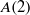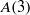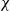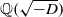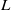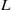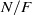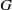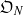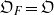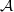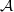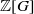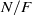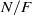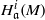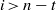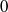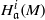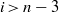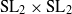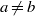Research Article
Residues of Eisenstein series and the automorphic cohomology of reductive groups
- Part of:
-
- Published online by Cambridge University Press:
- 07 May 2013, pp. 1061-1090
-
- Article
-
- You have access
- Export citation
Independence of
 $\ell $-adic Galois representations over function fields
$\ell $-adic Galois representations over function fields
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2013, pp. 1091-1107
-
- Article
-
- You have access
- Export citation
On lower bounds for the Ihara constants
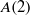 $A(2)$ and
$A(2)$ and 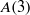 $A(3)$
$A(3)$
- Part of:
-
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1108-1128
-
- Article
-
- You have access
- Export citation
Pretentious multiplicative functions and the prime number theorem for arithmetic progressions
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 1129-1149
-
- Article
-
- You have access
- Export citation
Subconvexity and equidistribution of Heegner points in the level aspect
- Part of:
-
- Published online by Cambridge University Press:
- 17 June 2013, pp. 1150-1174
-
- Article
-
- You have access
- Export citation
Self-dual integral normal bases and Galois module structure
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2013, pp. 1175-1202
-
- Article
-
- You have access
- Export citation
Cohomological and projective dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2013, pp. 1203-1210
-
- Article
-
- You have access
- Export citation
Automorphisms of Drinfeld half-spaces over a finite field
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2013, pp. 1211-1224
-
- Article
-
- You have access
- Export citation
Rationality of fields of invariants for some representations of SL2 × SL2
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2013, pp. 1225-1234
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
COM volume 149 issue 7 Cover and Front matter
-
- Published online by Cambridge University Press:
- 04 July 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
COM volume 149 issue 7 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 July 2013, pp. b1-b2
-
- Article
-
- You have access
- Export citation