Article contents
Subconvexity and equidistribution of Heegner points in the level aspect
Published online by Cambridge University Press: 17 June 2013
Abstract
Let 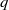 $q$ be a prime and
$q$ be a prime and 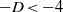 $- D\lt - 4$ be an odd fundamental discriminant such that
$- D\lt - 4$ be an odd fundamental discriminant such that 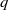 $q$ splits in
$q$ splits in 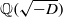 $ \mathbb{Q} ( \sqrt{- D} )$. For
$ \mathbb{Q} ( \sqrt{- D} )$. For 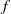 $f$ a weight-zero Hecke–Maass newform of level
$f$ a weight-zero Hecke–Maass newform of level 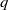 $q$ and
$q$ and 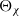 ${\Theta }_{\chi } $ the weight-one theta series of level
${\Theta }_{\chi } $ the weight-one theta series of level 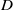 $D$ corresponding to an ideal class group character
$D$ corresponding to an ideal class group character 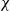 $\chi $ of
$\chi $ of 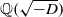 $ \mathbb{Q} ( \sqrt{- D} )$, we establish a hybrid subconvexity bound for
$ \mathbb{Q} ( \sqrt{- D} )$, we establish a hybrid subconvexity bound for 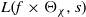 $L(f\times {\Theta }_{\chi } , s)$ at
$L(f\times {\Theta }_{\chi } , s)$ at 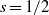 $s= 1/ 2$ when
$s= 1/ 2$ when 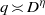 $q\asymp {D}^{\eta } $ for
$q\asymp {D}^{\eta } $ for 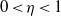 $0\lt \eta \lt 1$. With this circle of ideas, we show that the Heegner points of level
$0\lt \eta \lt 1$. With this circle of ideas, we show that the Heegner points of level 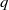 $q$ and discriminant
$q$ and discriminant 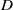 $D$ become equidistributed, in a natural sense, as
$D$ become equidistributed, in a natural sense, as 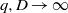 $q, D\rightarrow \infty $ for
$q, D\rightarrow \infty $ for 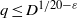 $q\leq {D}^{1/ 20- \varepsilon } $. Our approach to these problems is connected to estimating the
$q\leq {D}^{1/ 20- \varepsilon } $. Our approach to these problems is connected to estimating the 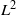 ${L}^{2} $-restriction norm of a Maass form of large level
${L}^{2} $-restriction norm of a Maass form of large level 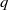 $q$ when restricted to the collection of Heegner points. We furthermore establish bounds for quadratic twists of Hecke–Maass
$q$ when restricted to the collection of Heegner points. We furthermore establish bounds for quadratic twists of Hecke–Maass 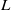 $L$-functions with simultaneously large level and large quadratic twist, and hybrid bounds for quadratic Dirichlet
$L$-functions with simultaneously large level and large quadratic twist, and hybrid bounds for quadratic Dirichlet 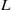 $L$-functions in certain ranges.
$L$-functions in certain ranges.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2013
References
- 16
- Cited by


