Research Article
Hilbert Rings Arising as Pullbacks
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 431-438
-
- Article
-
- You have access
- Export citation
Topological Completeness of Function Spaces Arising in the Hausdorff Approximation of Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 439-448
-
- Article
-
- You have access
- Export citation
Weakness of the Topology of a JB*-Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-454
-
- Article
-
- You have access
- Export citation
A Variational Characterization of Contact Metric Manifolds With Vanishing Torsion
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 455-462
-
- Article
-
- You have access
- Export citation
Sandwich Theorems for Semicontinuous Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 463-474
-
- Article
-
- You have access
- Export citation
Non-Archimedean t-Frames and FM-Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 475-483
-
- Article
-
- You have access
- Export citation
Conditions for the Separability of Objects in Two-Dimensional Velocity Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 484-491
-
- Article
-
- You have access
- Export citation
Finiteness Conditions for Near-Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 492-496
-
- Article
-
- You have access
- Export citation
Compact Sets in CP(X) and Calibers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 497-502
-
- Article
-
- You have access
- Export citation
Divisors on Varieties Over a Real Closed Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 503-509
-
- Article
-
- You have access
- Export citation
Centralizing Automorphisms of Lie Ideals in Prime Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 510-514
-
- Article
-
- You have access
- Export citation
Conorme et Inverse Généralisé Dans Les C*-Algèbres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 515-522
-
- Article
-
- You have access
- Export citation
Generalized Second Fundamental form for Lipschitzian Hypersurfaces by Way of Second Epi Derivatives
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 523-536
-
- Article
-
- You have access
- Export citation
Constructive Complete Distributivity III
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 537-547
-
- Article
-
- You have access
- Export citation
Connection Coefficients of Orthogonal Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 548-556
-
- Article
-
- You have access
- Export citation
Rigid Continua With Many Embeddings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 557-559
-
- Article
-
- You have access
- Export citation
An Easy Proof for Some Classical Theorems in Plane Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 560-568
-
- Article
-
- You have access
- Export citation

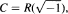 , with values in the Néron-Severi group and the Picard variety of
, with values in the Néron-Severi group and the Picard variety of  où a
où a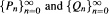 be polynomials orthogonal with respect to different distributions. Conditions are given which imply that the coefficients in the expansion of
be polynomials orthogonal with respect to different distributions. Conditions are given which imply that the coefficients in the expansion of 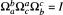 see the proof of the main theorem).
see the proof of the main theorem).