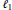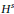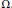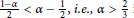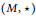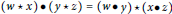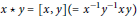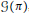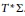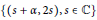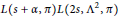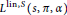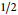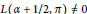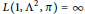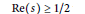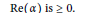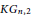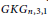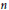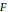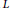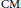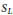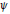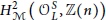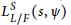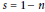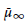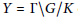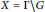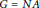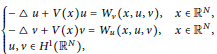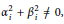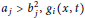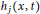Research Article
On the Graph of Divisibility of an Integral Domain
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-458
-
- Article
-
- You have access
- Export citation
Hyperplanes in the Space of Convergent Sequences and Preduals of ℓ1
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 459-470
-
- Article
-
- You have access
- Export citation
Almost Sure Global Well-posedness for the Fractional Cubic Schrödinger Equation on the Torus
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 471-485
-
- Article
-
- You have access
- Export citation
Inequalities for Partial Derivatives and their Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 486-496
-
- Article
-
- You have access
- Export citation
Constructing Double Magma on Groups Using Commutation Operations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 497-506
-
- Article
-
- You have access
- Export citation
VMO Space Associated with Parabolic Sections and its Application
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 507-518
-
- Article
-
- You have access
- Export citation
Refined Motivic Dimension
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 519-529
-
- Article
-
- You have access
- Export citation
Ricci Curvature Tensor and Non-Riemannian Quantities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 530-537
-
- Article
-
- You have access
- Export citation
Minimal Non Self Dual Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 538-547
-
- Article
-
- You have access
- Export citation
Higher Moments of Fourier Coefficients of Cusp Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 548-560
-
- Article
-
- You have access
- Export citation
Plane Lorentzian and Fuchsian Hedgehogs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 561-574
-
- Article
-
- You have access
- Export citation
The Diffeomorphism Type of Canonical Integrations of Poisson Tensors on Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 575-579
-
- Article
-
- You have access
- Export citation
A Specialisation of the Bump–Friedberg L-function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 580-595
-
- Article
-
- You have access
- Export citation
A Note on Planarity Stratification of Hurwitz Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 596-609
-
- Article
-
- You have access
- Export citation
Path Decompositions of Kneser and Generalized Kneser Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 610-619
-
- Article
-
- You have access
- Export citation
L-functions for Quadratic Characters and Annihilation of Motivic Cohomology Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 620-631
-
- Article
-
- You have access
- Export citation
Quantum Unique Ergodicity on Locally Symmetric Spaces: the Degenerate Lift
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 632-650
-
- Article
-
- You have access
- Export citation
Ground State Solutions of Nehari–Pankov Type for a Superlinear Hamiltonian Elliptic System on ℝN
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 651-663
-
- Article
-
- You have access
- Export citation
Betti Numbers and Flat Dimensions of Local Cohomology Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 664-672
-
- Article
-
- You have access
- Export citation