Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-25T05:50:25.117Z Has data issue: false hasContentIssue false
  • English
  • Français

The Diffeomorphism Type of Canonical Integrations of Poisson Tensors on Surfaces

Published online by Cambridge University Press:  20 November 2018

David Martínez Torres
David Martínez Torres*
Affiliation:
PUC-Rio de Janeiro, Departamento de Matemática, Gávea - 224151, Rio de Janeiro, Brazil e-mail: dfmtorres@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A surface $\sum$ endowed with a Poisson tensor $\pi$ is known to admit a canonical integration, 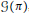$G\left( \pi \right)$, which is a 4-dimensional manifold with a (symplectic) Lie groupoid structure. In this short note we show that if $\text{ }\!\!\pi\!\!\text{ }$ is not an area form on the 2-sphere, then 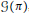$G\left( \pi \right)$ is diffeomorphic to the cotangent bundle 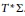$T*\sum$. This extends results by the author and by Bonechi, Ciccoli, Staffolani, and Tarlini.

Keywords

58H0555R1053D17Poisson tensorLie groupoidcotangent bundle
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 3 , 01 September 2015 , pp. 575 - 579
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Cattaneo, A. S. and Felder, G., Poisson sigma models and symplecticgroupoids.In: Quantization of singularsymplectic quotients, Progr. Math., 198, Birkhâuser, Basel, 2001, pp. 61–93.Google Scholar
[2] Bonechi, F., Ciccoli, N., Staffolani, N., and Tarlini, M., The quantization of the symplecticgroupoid of the standard Podles sphere. J. Geom. Phys. 62(2012), no. 8,1851–1865. http://dx.doi.Org/1 0.101 6/j.geomphys.2012.04.001 Google Scholar
[3] Crainic, M. and Fernandes, R. L., Integrability of Poisson brackets. J. Differential Geom. 66(2004), no. 1, 71–137.Google Scholar
[4] Crainic, M. and Màrcuf, I., On the existence of symplectic realizations. J. Symplectic Geom. 9(2011), no. 4, 435–444. http://dx.doi.org/10.4310/JSC.2011 .v9.n4.a2 Google Scholar
[5] Hawkins, E., A groupoid approach to quantization. J. Symplectic Geom. 6(2008), no. 1, 61–125. http://dx.doi.org/10.4310/JSC.2008.v6.n1.a4 Google Scholar
[6] Martinez Torres, D., A note on the separability of canonical integrations of Lie algebroids. Math. Res. Lett. 17(2010), no. 1, 69–75. http://dx.doi.org/10.4310/MRL.2010.v17.n1 .a6 Google Scholar
[7] McDuff, D., The symplectic structure ofKàhlermanifolds of nonpositive curvature. J. Differential Geom. 28(1988), no. 3, 467–475.Google Scholar
[8] McDuff, D. and Salamon, D., Introduction to symplectic topology. Second éd.,Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, New York, 1998.Google Scholar
[9] Meigniez, G., Submersions, fibrations and bundles. Trans. Amer. Math. Soc. 354(2002), no. 9, 3771–3787. http://dx.doi.org/10.1090/S0002-9947-02-02972-0 Google Scholar
[10] Weinstein, A., Symplecticgroupoids and Poisson manifolds. Bull. Amer. Math.Soc. (N.S.) 16(1987), no. 1, 101–104. http://dx.doi.org/10.1090/S0273-0979-1987-15473-5 Google Scholar