Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-24T05:08:01.344Z Has data issue: false hasContentIssue false
  • English
  • Français

VMO Space Associated with Parabolic Sections and its Application

Published online by Cambridge University Press:  20 November 2018

Ming-Hsiu Hsu  and
Ming-Yi Lee
Ming-Hsiu Hsu
Affiliation:
Department of Mathematics, National Central University, Chung-Li, 32054, Taiwan e-mail: hsumh@math.ncu.edu.twmylee@math.ncu.edu.tw
Ming-Yi Lee
Affiliation:
Department of Mathematics, National Central University, Chung-Li, 32054, Taiwan e-mail: hsumh@math.ncu.edu.twmylee@math.ncu.edu.tw
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we define a space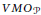$VM{{O}_{P}}$ associated with a family 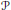$P$ of parabolic sections and show that the dual of 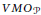$VM{{O}_{P}}$ is the Hardy space 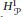$H_{P}^{1}$. As an application, we prove that almost everywhere convergence of a bounded sequence in 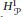$H_{P}^{1}$ implies weak$^{\star }$ convergence

Keywords

42B30Monge-Ampère equationparabolic sectionHardy spaceBMOVMO
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 3 , 01 September 2015 , pp. 507 - 518
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Aimar, H., Forzani, L., and Toledano, R., Balls and quasi-metrics: a space of homogeneous type modeling the real analysis related to the Monge-Ampère equation. J. Fourier Anal. Appl. 4(1998), no. 4-5, 377–381. http://dx.doi.org/10.1007/BF02498215 Google Scholar
[2] Caffarelli, L. A., Some regularity properties of solutions of Monge-Ampere equation. Comm. Pure Appl. Math. 44(1991), no. 8-9, 965–969. http://dx.doi.org/10.1002/cpa.3160440809 Google Scholar
[3] Caffarelli, L. A. , Boundary regularity of maps with convex potentials. Comm. Pure Appl. Math. 45(1992), no. 9, 1141–1151. http://dx.doi.org/10.1002/cpa.3160450905 Google Scholar
[4] Caffarelli, L. A. and Gutierrez, C. E., Real analysis related to the Monge-Ampère equation. Trans. Amer. Math. Soc. 348(1996), no. 3, 1075–1092. http://dx.doi.org/10.1090/S0002-9947-96-01473-0 Google Scholar
[5] Caffarelli, L. A. and Gutierrez, C. E., Properties of the solutions of the linearized Monge-Ampère equation. Amer. J. Math. 119(1997), no. 2, 423–465. http://dx.doi.org/10.1353/ajm.1997.0010 Google Scholar
[6] Coifman, R. and Weiss, G., Extensions of Hardy spaces and their use in analysis. Bull. Amer. Math. Soc. 83(1977), no. 4, 569–645. http://dx.doi.org/10.1090/S0002-9904-1977-14325-5 Google Scholar
[7] Coifman, R., Lions, P.-L., Meyer, Y., and Semmes, S., Compensated compactness and Hardy sapces. J. Math.Pures Appl. 72(1993), no. 3, 247–286.Google Scholar
[8] Ding, Y. and Lin, C.-C., Hardy spaces associated to the sections. Tohoku Math. J. 57(2005), no. 2, 147–170. http://dx.doi.Org/1 0.2748/tmj/111 9888333 Google Scholar
[9] Huang, Q., Harnack inequality for the linearized parabolic Monge-Ampère equation. Trans. Amer. Math. Soc. 351(1999), 2025–2054. http://dx.doi.org/10.1090/S0002-9947-99-02142-X Google Scholar
[10] Jones, P. W. and Journé, On weak convergence in H1^). Proc. Amer. Math. Soc. 120(1994), 137–138.Google Scholar
[11] Qu, M. and Wu, X., BMO spaces associated to generalized parabolic sections. Anal.Theory Appl. 27(2011), no. 1, 1–9. http://dx.doi.Org/10.1 007/s1 0496-011-0001 -2 Google Scholar
[12] Wu, X., Hardy spaces associated to generalized parabolic sections. Panamer.Math. J. 18(2008), no. 2, 33–51.Google Scholar