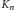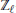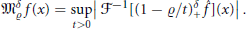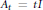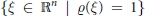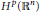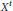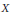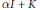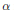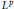Research Article
Answer to a Question of S. Rolewicz
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 161-163
-
- Article
-
- You have access
- Export citation
Classification of AF Flows
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 164-177
-
- Article
-
- You have access
- Export citation
Sur les invariants d'Iwasawa des tours cyclotomiques
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 178-190
-
- Article
-
- You have access
- Export citation
Weak Type Estimates of the Maximal Quasiradial Bochner-Riesz Operator On Certain Hardy Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 191-203
-
- Article
-
- You have access
- Export citation
Rationality and Orbit Closures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 204-215
-
- Article
-
- You have access
- Export citation
Linear Maps on Selfadjoint Operators Preserving Invertibility, Positive Definiteness, Numerical Range
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 216-228
-
- Article
-
- You have access
- Export citation
Counting the Number of Integral Points in General
 $n$-Dimensional Tetrahedra and Bernoulli Polynomials
$n$-Dimensional Tetrahedra and Bernoulli Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 229-241
-
- Article
-
- You have access
- Export citation
Euclidean Sections of Direct Sums of Normed Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 242-251
-
- Article
-
- You have access
- Export citation
Beurling-Dahlberg-Sjögren Type Theorems for Minimally Thin Sets in a Cone
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 252-264
-
- Article
-
- You have access
- Export citation
Reducing Spheres and Klein Bottles after Dehn Fillings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 265-267
-
- Article
-
- You have access
- Export citation
Group Cohomology and
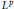 ${{L}^{p}}$-Cohomology of Finitely Generated Groups
${{L}^{p}}$-Cohomology of Finitely Generated Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 268-276
-
- Article
-
- You have access
- Export citation
Rigidity of Hamiltonian Actions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 277-290
-
- Article
-
- You have access
- Export citation
A Coincidence Theorem for Holomorphic Maps to
 $G/P$
$G/P$
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 291-298
-
- Article
-
- You have access
- Export citation
A Basis of Bachmuth Type in the Commutator Subgroup of a Free Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 299-303
-
- Article
-
- You have access
- Export citation
Localization of the Hasse-Schmidt Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 304-309
-
- Article
-
- You have access
- Export citation
Second Order Dehn Functions of Asynchronously Automatic Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 310-318
-
- Article
-
- You have access
- Export citation