Let 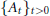${{\left\{ {{A}_{t}} \right\}}_{t>0}}$ be the dilation group in 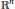${{\mathbb{R}}^{n}}$ generated by the infinitesimal generator 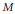$M$ where 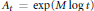${{A}_{t}}\,=\,\exp \left( M\,\log \,t \right)$, and let 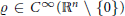$\varrho \,\in \,{{C}^{\infty }}\left( \mathbb{R}{{}^{n\,}}\backslash \,\left\{ 0 \right\} \right)$ be a 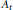${{A}_{t}}$-homogeneous distance function defined on 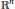${{\mathbb{R}}^{n}}$. For 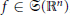$f\,\in \,\mathfrak{S}\left( \mathbb{R}{{}^{n}} \right)$, we define the maximal quasiradial Bochner-Riesz operator 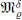$\mathfrak{M}_{\varrho }^{\delta }$ of index 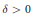$\delta \,>\,0$ by

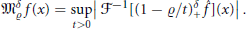$$\mathfrak{M}_{\varrho }^{\delta }f\left( x \right)\,=\,\underset{t>0}{\mathop{\sup }}\,\left| {{\mathcal{F}}^{-1}}\left[ \left( 1-{\varrho }/{t}\; \right)_{+}^{\delta }\hat{f} \right]\left( x \right) \right|.$$

If 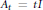${{A}_{t\,}}=\,tI$ and 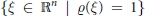$\left\{ \xi \,\in \,{{\mathbb{R}}^{n\,}}\,|\,\varrho \left( \xi \right)\,=\,1 \right\}$ is a smooth convex hypersurface of finite type, then we prove in an extremely easy way that 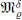$\mathfrak{M}_{\varrho }^{\delta }$ is well defined on 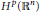${{H}^{p}}\left( {{\mathbb{R}}^{n}} \right)$ when 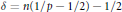$\delta \,=\,n(1/p\,-\,1/2)\,-\,1/2$ and 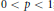$0\,<\,p\,<\,1$; moreover, it is a bounded operator from 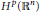${{H}^{p}}\left( {{\mathbb{R}}^{n}} \right)$ into 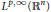${{L}^{p,\infty }}\left( {{\mathbb{R}}^{n}} \right)$ .

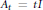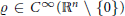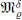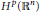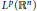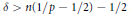If ${{A}_{t}}\,=\,tI$ and $\varrho \,\in \,{{C}^{\infty }}\left( \mathbb{R}{{}^{n\,}}\backslash \,\left\{ 0 \right\} \right)$ , we also prove that $\mathfrak{M}_{\varrho }^{\delta }$ is a bounded operator from ${{H}^{p}}\left( {{\mathbb{R}}^{n}} \right)$ into ${{L}^{p}}\,\left( {{\mathbb{R}}^{n}} \right)$ when $\delta \,>\,n(1/p\,-\,1/2)\,-\,1/2$ and 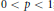$0\,<\,p\,<\,1$.