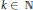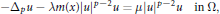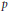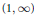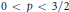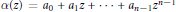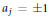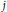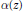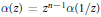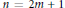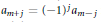Research Article
Polygons with Prescribed Gauss Map in Hadamard Spaces and Euclidean Buildings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 321-336
-
- Article
-
- You have access
- Export citation
Homotopy Equivalence and Groups of Measure-Preserving Homeomorphisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 337-346
-
- Article
-
- You have access
- Export citation
Affine Completeness of Generalised Dihedral Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 347-357
-
- Article
-
- You have access
- Export citation
On the Principal Eigencurve of the p-Laplacian: Stability Phenomena
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 358-370
-
- Article
-
- You have access
- Export citation
Inner E0-Semigroups on Infinite Factors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 371-380
-
- Article
-
- You have access
- Export citation
On the Membership in Bergman Spaces of the Derivative of a Blaschke Product With Zeros in a Stolz Domain
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 381-388
-
- Article
-
- You have access
- Export citation
A Free Logarithmic Sobolev Inequality on the Circle
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 389-406
-
- Article
-
- You have access
- Export citation
Intermediate Model Structures for Simplicial Presheaves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 407-413
-
- Article
-
- You have access
- Export citation
Commutators Estimates on Triebel–Lizorkin Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 414-427
-
- Article
-
- You have access
- Export citation
Vector-Valued Modular Forms of Weight Two Associated With Jacobi-Like Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 428-437
-
- Article
-
- You have access
- Export citation
Unimodular Roots of Special Littlewood Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 438-447
-
- Article
-
- You have access
- Export citation
A Lower Bound on the Number of Cyclic Function Fields With Class Number Divisible by n
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 448-463
-
- Article
-
- You have access
- Export citation
A Note on Detecting Algebraic Cycles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 464-471
-
- Article
-
- You have access
- Export citation
Cyclic Cubic Fields of Given Conductor and Given Index
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 472-480
-
- Article
-
- You have access
- Export citation