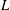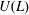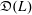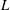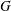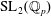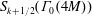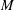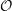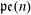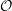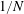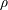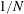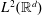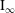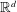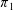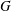Article
Mixed Perverse Sheaves on Flag Varieties for Coxeter Groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1-55
-
- Article
- Export citation
Local Convergence and Stability of Tight Bridge-addable Classes
- Part of:
-
- Published online by Cambridge University Press:
- 15 October 2018, pp. 563-601
-
- Article
- Export citation
The Action of a Plane Singular Holomorphic Flow on a Non-invariant Branch
- Part of:
-
- Published online by Cambridge University Press:
- 22 April 2019, pp. 835-866
-
- Article
- Export citation
Isospectrality for Orbifold Lens Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 281-325
-
- Article
- Export citation
Slice-torus Concordance Invariants and Whitehead Doubles of Links
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2019, pp. 1423-1462
-
- Article
- Export citation
On Some Generalized Rapoport–Zink Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 03 May 2019, pp. 1111-1187
-
- Article
- Export citation
Free Group Algebras in Division Rings with Valuation II
- Part of:
-
- Published online by Cambridge University Press:
- 05 July 2019, pp. 1463-1504
-
- Article
- Export citation
Ramification of the Eigencurve at Classical RM Points
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2019, pp. 57-88
-
- Article
- Export citation
Simultaneous Upper Triangular Forms for Commuting Operators in a Finite von Neumann Algebra
- Part of:
-
- Published online by Cambridge University Press:
- 15 May 2019, pp. 1188-1245
-
- Article
- Export citation
The Weak Order on Weyl Posets
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 867-899
-
- Article
- Export citation
On the First Zassenhaus Conjecture and Direct Products
- Part of:
-
- Published online by Cambridge University Press:
- 15 October 2018, pp. 602-624
-
- Article
- Export citation
Newforms of Half-integral Weight: The Minus Space Counterpart
- Part of:
-
- Published online by Cambridge University Press:
- 31 October 2019, pp. 326-372
-
- Article
- Export citation
The Primitive Spectrum and Category
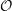 ${\mathcal{O}}$ for the Periplectic Lie Superalgebra
${\mathcal{O}}$ for the Periplectic Lie Superalgebra
- Part of:
-
- Published online by Cambridge University Press:
- 16 November 2018, pp. 625-655
-
- Article
- Export citation
Bakry–Émery Curvature Functions on Graphs
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 89-143
-
- Article
- Export citation
Marginals with Finite Repulsive Cost
- Part of:
-
- Published online by Cambridge University Press:
- 07 May 2019, pp. 373-391
-
- Article
- Export citation
A Measurable Selector in Kadison’s Carpenter’s Theorem
- Part of:
-
- Published online by Cambridge University Press:
- 16 July 2019, pp. 1505-1528
-
- Article
- Export citation
The Classification of 7- and 8-dimensional Naturally Reductive Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2019, pp. 1246-1274
-
- Article
- Export citation
On the Fourier Transformability of Strongly Almost Periodic Measures
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 900-927
-
- Article
- Export citation
Non-cocompact Group Actions and
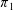 $\unicode[STIX]{x1D70B}_{1}$-Semistability at Infinity
$\unicode[STIX]{x1D70B}_{1}$-Semistability at Infinity
- Part of:
-
- Published online by Cambridge University Press:
- 26 June 2019, pp. 1275-1303
-
- Article
- Export citation
Automatic Sequences and Generalised Polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2019, pp. 392-426
-
- Article
- Export citation