Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T23:43:26.472Z Has data issue: false hasContentIssue false
  • English
  • Français

The Action of a Plane Singular Holomorphic Flow on a Non-invariant Branch

Part of: Singularities Curves

Published online by Cambridge University Press:  22 April 2019

P. Fortuny Ayuso  and
J. Ribón
P. Fortuny Ayuso
Affiliation:
Dpt. of Mathematics, Univ. of Oviedo, Spain Email: fortunypedro@uniovi.es
J. Ribón
Affiliation:
Dpt. of Analysis, Univ. Federal Fluminense, Brazil Email: jribon@id.uff.br
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the dynamics of a singular holomorphic vector field at 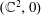$(\mathbb{C}^{2},0)$. Using the associated flow and its pullback to the blow-up manifold, we provide invariants relating the vector field, a non-invariant analytic branch of curve, and the deformation of this branch by the flow. This leads us to study the conjugacy classes of singular branches under the action of holomorphic flows. In particular, we show that there exists an analytic class that is not complete, meaning that there are two elements of the class that are not analytically conjugated by a local biholomorphism embedded in a one-parameter flow. Our techniques are new and offer an approach dual to the one used classically to study singularities of holomorphic vector fields.

Keywords

holomorphic vector fielddeformationmoduliplane branch

MSC classification

Primary: 32S05: Local singularities
Secondary: 32S65: Singularities of holomorphic vector fields and foliations 14H20: Singularities, local rings
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 4 , August 2020 , pp. 835 - 866
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Both authors are partially supported by Ministerio de Economía y Competitividad, Spain, process MTM2016-77642-C2-1-P.

References

Brunella, M., Birational geometry of foliations. IMPA Monographs, 1, Springer, Cham, 2015. https://doi.org/10.1007/978-3-319-14310-1Google Scholar
Camacho, C., Lins-Neto, A., and Sad, P., Topological invariants and equidesingularization for holomorphic vector fields. J. Differential Geom. 20(1984), 143–174.10.4310/jdg/1214438995Google Scholar
Camacho, C. and Sad, P., Invariant varieties through singularities of holomorphic vector fields. Ann. of Math. 115(1982), 579–595. https://doi.org/10.2307/2007013Google Scholar
Cano Torres, F., Desingularization strategies for three-dimensional vector fields. Lecture Notes in Mathematics, 1259, Springer-Verlag, Berlin, 1987. https://doi.org/10.1007/BFb0077952Google Scholar
Cano, F., Moussu, R., and Rolin, J.-P., Non-oscillating integral curves and valuations. J. Reine Angew. Math. 582(2005), 107–142. https://doi.org/10.1515/crll.2005.2005.582.107Google Scholar
Cano, F., Moussu, R., and Sanz, F., Oscillation, spiralement, tourbillonnement. Comment. Math. Helv. 75(2000), 284–318. https://doi.org/10.1007/s000140050127Google Scholar
Cano, F., Roche, C., and Spivakovsky, M., Reduction of singularities of three-dimensional line foliations. Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. RACSAM 108(2010), 221–258. https://doi.org/10.1007/s13398-013-0117-7Google Scholar
Casas-Alvero, E., Singularities of plane curves. London Mathematical Society Lecture Notes Series, 276, Cambridge University Press, Cambridge, 2000. https://doi.org/10.1017/CBO9780511569326Google Scholar
Écalle, J., Théorie itérative: introduction à la théorie des invariants holomorphes. J. Math. Pures Appl. (9) 54(1975), 183–258.Google Scholar
Greuel, G. M., Lossen, C., and Shustin, E. I., Introduction to singularities and deformations. Springer Monographs in Mathematics, Springer, Berlin, 2007.Google Scholar
Hefez, A. and Hernandes, M. E., The analytic classification of plane branches. Bull. Lond. Math. Soc. 43(2011), 289–298. https://doi.org/10.1112/blms/bdq113Google Scholar
Ilyashenko, Y. and Yakovenko, S., Lectures on analytic differential equations. Graduate Studies in Mathematics, 86, American Mathematical Society, Providence, RI, 2008.Google Scholar
Martinet, J. and Ramis, J.-P., Classification analytique des équations différentielles non linéaires résonnantes du premier ordre. Ann. Scient. Éc. Norm. Sup. 16(1983), 571–621.10.24033/asens.1462Google Scholar
Brochero Martínez, F. E., Cano, F., and López-Hernanz, L., Parabolic curves for diffeomorphisms in ℂ2. Publ. Mat. 52(2008), 189–194. https://doi.org/10.5565/PUBLMAT_52108_09Google Scholar
Mattei, J. F. and Moussu, R., Holonomie et intégrales premières. Ann. Sci. Ec. Norm. Sup. 13(1980), 469–523.10.24033/asens.1393Google Scholar
Ribón, J., Embedding smooth and formal diffeomorphisms through the jordan–chevalley decomposition. J. Differential Equations 253(2012), 3211–3231. https://doi.org/10.1016/j.jde.2012.09.009Google Scholar
Seidenberg, A., Reduction of singularities of the differential equation Ady = Bdx. Amer. J. Math. 90(1968), 248–269. https://doi.org/10.2307/2373435Google Scholar
Wall, C. T. C., Singular points of plane curves. London Mathematical Society Student Texts, 63, Cambridge University Press, 2009. https://doi.org/10.1017/CBO9780511617560Google Scholar
Zariski, O., Le problème des modules pour les branches planes. École Polytechnique, Paris, 1973.Google Scholar
Zhang, X., The embedding flows of 𝓒∞ hyperbolic diffeomorphisms. J. Differential Equations 250(2011), 2283–2298. https://doi.org/10.1016/j.jde.2010.12.022Google Scholar