Research Article
Einstein-Kaehler Manifolds Immersed in a Complex Projective Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-8
-
- Article
-
- You have access
- Export citation
On the Endomorphisms of a Polynomial Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 9-18
-
- Article
-
- You have access
- Export citation
Operators of Rank One in Reflexive Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 19-23
-
- Article
-
- You have access
- Export citation
On a Theorem of Kuiper
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 24-41
-
- Article
-
- You have access
- Export citation
Boundaries For Real Banach Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 42-49
-
- Article
-
- You have access
- Export citation
Pure Compactifications in Quasi-Primal Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 50-62
-
- Article
-
- You have access
- Export citation
Isometry of Riemannian Manifolds to Spheres, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 63-72
-
- Article
-
- You have access
- Export citation
Modules Over Hereditary Noetherian Prime Rings, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 73-82
-
- Article
-
- You have access
- Export citation
An Application of Logic to Analysis
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 83-91
-
- Article
-
- You have access
- Export citation
A Counterexample to a Classification Theorem of Linearly Stable Polytopes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 92-93
-
- Article
-
- You have access
- Export citation
Finite Rings in Which 1 is a Sum of Two Non-P-Th Power Units
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 94-103
-
- Article
-
- You have access
- Export citation
Uniform And Tangential Approximations By Meromorphic Functions on Closed Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 104-111
-
- Article
-
- You have access
- Export citation
Possibility of Uniform Rational Approximation in the Spherical Metric
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 112-115
-
- Article
-
- You have access
- Export citation
On Translation Planes with Affine Central Collineations, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 116-129
-
- Article
-
- You have access
- Export citation
Factor Representations and Factor States on a C*-Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 130-134
-
- Article
-
- You have access
- Export citation
Coding Ergodic Processes to Approximate Bernoulli Processes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 135-140
-
- Article
-
- You have access
- Export citation
On Nonstandard Hulls of Convex Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 141-147
-
- Article
-
- You have access
- Export citation
Weakly Regular Algebras, Boolean Orthogonalities and Direct Products of Integral Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 148-153
-
- Article
-
- You have access
- Export citation
An Induction Theorem for Rearrangements
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 154-160
-
- Article
-
- You have access
- Export citation
Minimal Plat Representations of Prime Knots and Links are not Unique
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 161-167
-
- Article
-
- You have access
- Export citation



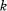 . Suppose there is a subring
. Suppose there is a subring 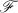 is a collection of (closed linear) subspaces of
is a collection of (closed linear) subspaces of 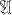
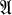
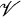 for which every
for which every 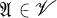 can be purely embedded in an equationally compact algebra
can be purely embedded in an equationally compact algebra 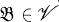 , and for all notions not explained here, the reader is referred to [
, and for all notions not explained here, the reader is referred to [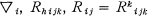 and
and 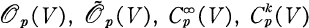 be the germs at
be the germs at 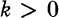 such that
such that 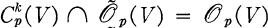 , generalizing the result of Malgrange [12] that
, generalizing the result of Malgrange [12] that 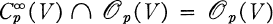 .In [
.In [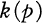 is bounded on compact sets. Bloom [
is bounded on compact sets. Bloom [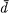 on processes which, for processes (P, τ) and
on processes which, for processes (P, τ) and 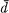 ((P,
((P,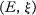 is a standard TVS
is a standard TVS 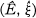 constructed from a nonstandard model for
constructed from a nonstandard model for 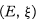 [
[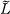 denote the 2-fold cyclic covering space branched over a link
denote the 2-fold cyclic covering space branched over a link 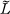 are minimal and inequivalent. Thus each knot or link of that family admits at least two equivalence classes of 6-plat representations which are minimal.
are minimal and inequivalent. Thus each knot or link of that family admits at least two equivalence classes of 6-plat representations which are minimal.