Research Article
Involutory Matrices Over Finite Local Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 369-378
-
- Article
-
- You have access
- Export citation
Uniformities on a Product
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 379-389
-
- Article
-
- You have access
- Export citation
On Strong Nörlund Summability Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 390-399
-
- Article
-
- You have access
- Export citation
Ideals and Higher Derivations in Commutative Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 400-415
-
- Article
-
- You have access
- Export citation
Familles De Valuations A Caractere Compact
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 416-425
-
- Article
-
- You have access
- Export citation
A Generalization of “Concordance of PL-Homeomorphisms of Sp × Sq
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 426-431
-
- Article
-
- You have access
- Export citation
Condition that All Irreducible Representations of a Compact Lie Group, if Restricted to a Subgroup, Contain no Representation More than Once
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 432-438
-
- Article
-
- You have access
- Export citation
S-Maximal Subgroups of πl(M3)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 439-449
-
- Article
-
- You have access
- Export citation
The Torsion Submodule of A Cyclic Module Splits Off
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 450-464
-
- Article
-
- You have access
- Export citation
Projective Homotopy Classes of Stiefel Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 465-476
-
- Article
-
- You have access
- Export citation
On Multipliers with Unconditionally Converging Fourier Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 477-484
-
- Article
-
- You have access
- Export citation
C(X) As A Dual Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 485-491
-
- Article
-
- You have access
- Export citation
Extended Chromatic Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 492-501
-
- Article
-
- You have access
- Export citation
Intersections of Primary Ideals in Rings of Continuous Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 502-519
-
- Article
-
- You have access
- Export citation
Positive Linear Maps on C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 520-529
-
- Article
-
- You have access
- Export citation
A Universal Property of the Takahashi Quasi-Dual
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 530-536
-
- Article
-
- You have access
- Export citation
A Note on Complementary Subspaces in c0
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 537-540
-
- Article
-
- You have access
- Export citation
On the Plethysm of S-Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 541-552
-
- Article
-
- You have access
- Export citation



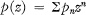 wherever this series converges. (Where no limits are stated, sums are throughout to be taken from
wherever this series converges. (Where no limits are stated, sums are throughout to be taken from 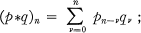
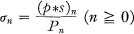
 , l'anneau de la valuation
, l'anneau de la valuation  , l'idéal maximal de l'anneau
, l'idéal maximal de l'anneau  l'anneau défini par la famille Ω; nous supposons toujours Ω tel que
l'anneau défini par la famille Ω; nous supposons toujours Ω tel que  et munissons Ω de la topologie la plus faible pour laquelle les
et munissons Ω de la topologie la plus faible pour laquelle les 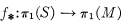
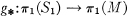 is an injection,
is an injection,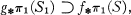
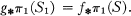 Then we shall say that the subgroup
Then we shall say that the subgroup 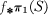 is a
is a 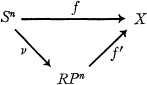
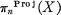 the subset of projective homotopy classes in
the subset of projective homotopy classes in 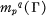 denote the Banach space of complex-valued functions on Γ which are multipliers of type
denote the Banach space of complex-valued functions on Γ which are multipliers of type 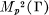 (Theorem 2.1), and that, for 1 ≦
(Theorem 2.1), and that, for 1 ≦ 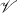 (
(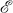 (
(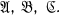 . Capital letters
. Capital letters 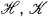 for vector spaces, small letters x,
for vector spaces, small letters x, 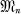 the collection of all
the collection of all 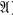 ) =
) =