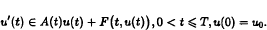Research Article
Équations de Fermat de type (5, 5,p)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-194
-
- Article
-
- You have access
- Export citation
A periodic wavelet method for the second kind of the logarithmic integral equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-336
-
- Article
-
- You have access
- Export citation
On inequalities of Hilbert's type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-13
-
- Article
-
- You have access
- Export citation
Perturbation theory of multivalued atkinson operators in normed spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 195-204
-
- Article
-
- You have access
- Export citation
A note on Nk configurations and theorems in projective space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 15-31
-
- Article
-
- You have access
- Export citation
Analysis of a periodic bacteria-immunity system with delayed quorum sensing
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 337-351
-
- Article
-
- You have access
- Export citation
Composition operators on Lorentz spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 205-214
-
- Article
-
- You have access
- Export citation
Sign-variations of solutions of nonlinear discrete boundary value problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 33-42
-
- Article
-
- You have access
- Export citation
A sequential quadratic programming algorithm for nonlinear minimax problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-368
-
- Article
-
- You have access
- Export citation
An analytic extension of a spacelike maximal surface
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 43-47
-
- Article
-
- You have access
- Export citation
A Remark on minimal Lagrangian diffeomorphisms and the Monge-Ampère equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 215-218
-
- Article
-
- You have access
- Export citation
Semi-classical solutions for a nonlinear coupled elliptic-parabolic problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 369-396
-
- Article
-
- You have access
- Export citation
The 2-epistasis of fitness functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 397-419
-
- Article
-
- You have access
- Export citation
A note on the theorem of Baturov
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 219-225
-
- Article
-
- You have access
- Export citation
Completely continuous elements of Banach algebras related to locally compact groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 49-54
-
- Article
-
- You have access
- Export citation
Existence results for semilinear differential inclusions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 227-241
-
- Article
-
- You have access
- Export citation
The Symplecticity of the Magnus Representation for Homology Cobordisms of Surfaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 421-431
-
- Article
-
- You have access
- Export citation
A rank for right congruences on inverse semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 55-68
-
- Article
-
- You have access
- Export citation
On the Powers of Some Transcendental Numbers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 433-440
-
- Article
-
- You have access
- Export citation
Generalised symmetries of partial differential equations via complex transformations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 243-262
-
- Article
-
- You have access
- Export citation

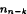 “theorem” about projective space (over a field or skew-field
“theorem” about projective space (over a field or skew-field 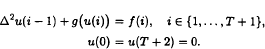 We establish the relationship between the number of sign-variation of
We establish the relationship between the number of sign-variation of 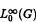 be the Banach space of all essentially bounded measurable functions on
be the Banach space of all essentially bounded measurable functions on 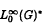 equipped with an Arens type product. As the main result, we show that
equipped with an Arens type product. As the main result, we show that