Article contents
Existence results for semilinear differential inclusions
Published online by Cambridge University Press: 17 April 2009
Extract
In this paper we study the existence of mild solutions for Cauchy problem
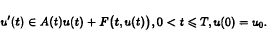
We derive conditions under which the mild solutions exist, and also get the relative compactness of the solution set, which extend and improve some existing results in this area.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 76 , Issue 2 , October 2007 , pp. 227 - 241
- Copyright
- Copyright © Australian Mathematical Society 2007
References
- 3
- Cited by


