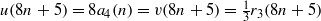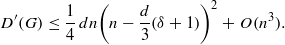Research Article
BIPARTITE DIVISOR GRAPH FOR THE PRODUCT OF SUBSETS OF INTEGERS
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2012, pp. 288-297
-
- Article
-
- You have access
- Export citation
HEISENBERG–PAULI–WEYL UNCERTAINTY INEQUALITY FOR THE DUNKL TRANSFORM ON ℝd
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2012, pp. 316-325
-
- Article
-
- You have access
- Export citation
INFINITE FAMILIES OF ARITHMETIC IDENTITIES FOR 4-CORES
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2012, pp. 304-315
-
- Article
-
- You have access
- Export citation
ARENS REGULARITY AND AMENABILITY OF LAU PRODUCT OF BANACH ALGEBRAS DEFINED BY A BANACH ALGEBRA MORPHISM
- Part of:
-
- Published online by Cambridge University Press:
- 31 July 2012, pp. 195-206
-
- Article
-
- You have access
- Export citation
P-SPACES AND THE VOLTERRA PROPERTY
- Part of:
-
- Published online by Cambridge University Press:
- 31 July 2012, pp. 339-345
-
- Article
-
- You have access
- Export citation
CLASSIFICATION OF QUIVER HOPF ALGEBRAS AND POINTED HOPF ALGEBRAS OF TYPE ONE
-
- Published online by Cambridge University Press:
- 06 August 2012, pp. 216-237
-
- Article
-
- You have access
- Export citation
GENERATING SYSTEMS OF SUBGROUPS IN SU(2, 1)
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2012, pp. 346-352
-
- Article
-
- You have access
- Export citation
VARIETIES WHOSE TOLERANCES ARE HOMOMORPHIC IMAGES OF THEIR CONGRUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 08 August 2012, pp. 326-338
-
- Article
-
- You have access
- Export citation
EXISTENCE OF NONINNER AUTOMORPHISMS OF ORDER p IN SOME FINITE p-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2012, pp. 272-277
-
- Article
-
- You have access
- Export citation
DEGREE DISTANCE AND MINIMUM DEGREE
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2012, pp. 255-271
-
- Article
-
- You have access
- Export citation
ON THE EXISTENCE OF NONINNER AUTOMORPHISMS OF ORDER TWO IN FINITE 2-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2012, pp. 278-287
-
- Article
-
- You have access
- Export citation
SOME REVERSES OF THE JENSEN INEQUALITY WITH APPLICATIONS
-
- Published online by Cambridge University Press:
- 07 February 2013, pp. 177-194
-
- Article
-
- You have access
- Export citation
A NEW PROOF OF THE REALISATION OF CUBIC TABLEAUX
-
- Published online by Cambridge University Press:
- 25 January 2013, pp. 207-215
-
- Article
-
- You have access
- Export citation
ON PSEUDO
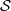 $ \mathcal{S} $-ASYMPTOTICALLY PERIODIC FUNCTIONS
$ \mathcal{S} $-ASYMPTOTICALLY PERIODIC FUNCTIONS
-
- Published online by Cambridge University Press:
- 30 January 2013, pp. 238-254
-
- Article
-
- You have access
- Export citation
DUNKL–WILLIAMS INEQUALITIES FOR INTEGRABLE FUNCTIONS IN BANACH SPACE
-
- Published online by Cambridge University Press:
- 12 December 2012, pp. 298-303
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
BAZ VOLUME 87 ISSUE 2 COVER AND BACK MATTER
-
- Published online by Cambridge University Press:
- 12 March 2013, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
BAZ VOLUME 87 ISSUE 2 COVER AND FRONT MATTER
-
- Published online by Cambridge University Press:
- 12 March 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation