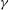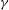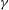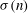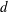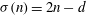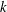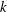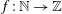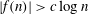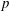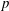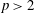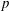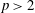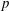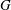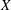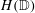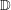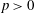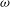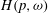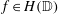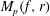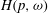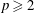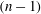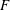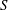Research Article
ON
 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\gamma $-VECTORS AND THE DERIVATIVES OF THE TANGENT AND SECANT FUNCTIONS
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\gamma $-VECTORS AND THE DERIVATIVES OF THE TANGENT AND SECANT FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 10 April 2014, pp. 177-185
-
- Article
-
- You have access
- Export citation
ON DEFICIENT-PERFECT NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2014, pp. 186-194
-
- Article
-
- You have access
- Export citation
THE MINIMAL GROWTH OF A
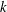 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2014, pp. 195-203
-
- Article
-
- You have access
- Export citation
GENERALISATION OF KEITH’S CONJECTURE ON 9-REGULAR PARTITIONS AND 3-CORES
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2014, pp. 204-212
-
- Article
-
- You have access
- Export citation
A NOTE ON INTERPOLATION OF PERMUTATIONS OF A SUBSET OF A FINITE FIELD
- Part of:
-
- Published online by Cambridge University Press:
- 15 May 2014, pp. 213-219
-
- Article
-
- You have access
- Export citation
ON A CLASS OF SUPERSOLUBLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2014, pp. 220-226
-
- Article
-
- You have access
- Export citation
ON NONINNER 2-AUTOMORPHISMS OF FINITE 2-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2014, pp. 227-231
-
- Article
-
- You have access
- Export citation
NONINNER AUTOMORPHISMS OF ORDER
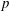 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ IN FINITE
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ IN FINITE 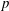 $p$-GROUPS OF COCLASS 2, WHEN
$p$-GROUPS OF COCLASS 2, WHEN 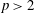 $p>2$
$p>2$
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2014, pp. 232-236
-
- Article
-
- You have access
- Export citation
ON A PROBLEM OF P. HALL FOR ENGEL WORDS II
- Part of:
-
- Published online by Cambridge University Press:
- 13 May 2014, pp. 237-246
-
- Article
-
- You have access
- Export citation
ON SOLUBILITY OF GROUPS WITH FEW NORMALISERS
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2014, pp. 247-249
-
- Article
-
- You have access
- Export citation
SOLVABILITY OF FINITE GROUPS WITH FOUR CONJUGACY CLASS SIZES OF CERTAIN ELEMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 21 July 2014, pp. 250-256
-
- Article
-
- You have access
- Export citation
BORNOLOGIES AND LOCALLY LIPSCHITZ FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 15 May 2014, pp. 257-263
-
- Article
-
- You have access
- Export citation
SOME RESULTS ON COMPARING TWO INTEGRAL MEANS FOR ABSOLUTELY CONTINUOUS FUNCTIONS AND APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 10 April 2014, pp. 264-274
-
- Article
-
- You have access
- Export citation
CHARACTERISATIONS OF HARDY GROWTH SPACES WITH DOUBLING WEIGHTS
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2014, pp. 275-282
-
- Article
-
- You have access
- Export citation
CARLEMAN ESTIMATE AND UNIQUE CONTINUATION PROPERTY FOR THE LINEAR STOCHASTIC KORTEWEG–DE VRIES EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 05 June 2014, pp. 283-294
-
- Article
-
- You have access
- Export citation
BARRELLED SPACES WITH(OUT) SEPARABLE QUOTIENTS
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2014, pp. 295-303
-
- Article
-
- You have access
- Export citation
A FURTHER PROPERTY OF SPHERICAL ISOMETRIES
- Part of:
-
- Published online by Cambridge University Press:
- 15 May 2014, pp. 304-310
-
- Article
-
- You have access
- Export citation
DOMINATION BY POSITIVE WEAK
 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}^{*}$ DUNFORD–PETTIS OPERATORS ON BANACH LATTICES
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}^{*}$ DUNFORD–PETTIS OPERATORS ON BANACH LATTICES
- Part of:
-
- Published online by Cambridge University Press:
- 05 June 2014, pp. 311-318
-
- Article
-
- You have access
- Export citation
AN EXISTENCE RESULT FOR A VARIATIONAL-LIKE INEQUALITY
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2014, pp. 319-326
-
- Article
-
- You have access
- Export citation
STATISTICAL CAUSALITY AND MARTINGALE REPRESENTATION PROPERTY WITH APPLICATION TO STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2014, pp. 327-338
-
- Article
-
- You have access
- Export citation