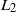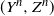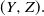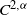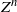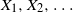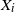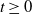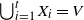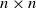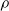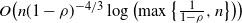Original Article
Limit theorems for process-level Betti numbers for sparse and critical regimes
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2020, pp. 1-31
-
- Article
- Export citation
Limit theorems for sequential MCMC methods
- Part of:
-
- Published online by Cambridge University Press:
- 15 July 2020, pp. 377-403
-
- Article
- Export citation
Exact simulation for multivariate Itô diffusions
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1003-1034
-
- Article
- Export citation
Almost sure central limit theorems in stochastic geometry
- Part of:
-
- Published online by Cambridge University Press:
- 24 September 2020, pp. 705-734
-
- Article
- Export citation
Transient analysis for exponential time-limited polling models under the preemptive repeat random policy
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2020, pp. 32-60
-
- Article
- Export citation
Limit theorems for assortativity and clustering in null models for scale-free networks
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1035-1084
-
- Article
- Export citation
Fluctuation identities for Omega-killed spectrally negative Markov additive processes and dividend problem
- Part of:
-
- Published online by Cambridge University Press:
- 15 July 2020, pp. 404-432
-
- Article
- Export citation
Mean square rate of convergence for random walk approximation of forward-backward SDEs
- Part of:
-
- Published online by Cambridge University Press:
- 24 September 2020, pp. 735-771
-
- Article
- Export citation
Geometric functionals of fractal percolation
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1085-1126
-
- Article
- Export citation
Out-of-equilibrium random walks
- Part of:
-
- Published online by Cambridge University Press:
- 24 September 2020, pp. 772-797
-
- Article
- Export citation
Speed and concentration of the covering time for structured coupon collectors
- Part of:
-
- Published online by Cambridge University Press:
- 15 July 2020, pp. 433-462
-
- Article
- Export citation
A non-exponential extension of Sanov’s theorem via convex duality
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2020, pp. 61-101
-
- Article
- Export citation
Limit theorems for multi-type general branching processes with population dependence
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1127-1163
-
- Article
- Export citation
An elementary derivation of moments of Hawkes processes
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2020, pp. 102-137
-
- Article
- Export citation
Stability and moment bounds under utility-maximising service allocations: Finite and infinite networks
- Part of:
-
- Published online by Cambridge University Press:
- 15 July 2020, pp. 463-490
-
- Article
- Export citation
Improved queue-size scaling for input-queued switches via graph factorization
- Part of:
-
- Published online by Cambridge University Press:
- 24 September 2020, pp. 798-824
-
- Article
- Export citation
Ergodicity of affine processes on the cone of symmetric positive semidefinite matrices
- Part of:
-
- Published online by Cambridge University Press:
- 24 September 2020, pp. 825-854
-
- Article
- Export citation
Samples with a limit shape, multivariate extremes, and risk
- Part of:
-
- Published online by Cambridge University Press:
- 15 July 2020, pp. 491-522
-
- Article
- Export citation
Thinning and multilevel Monte Carlo methods for piecewise deterministic (Markov) processes with an application to a stochastic Morris–Lecar model
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2020, pp. 138-172
-
- Article
- Export citation
Draw-down Parisian ruin for spectrally negative Lévy processes
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1164-1196
-
- Article
- Export citation