Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-24T21:34:15.170Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodicity of affine processes on the cone of symmetric positive semidefinite matrices

Part of: Ergodic theory Markov processes Stochastic processes

Published online by Cambridge University Press:  24 September 2020

Martin Friesen ,
Peng Jin ,
Jonas Kremer  and
Barbara Rüdiger
Martin Friesen*
Affiliation:
University of Wuppertal
Peng Jin*
Affiliation:
Shantou University
Jonas Kremer*
Affiliation:
University of Wuppertal
Barbara Rüdiger*
Affiliation:
University of Wuppertal
*
*Postal address: School of Mathematics and Natural Sciences, University of Wuppertal, 42119 Wuppertal, Germany. E-mail address: friesen@math.uni-wuppertal.de
**Postal address: Department of Mathematics, Shantou University, Shantou, Guangdong 515063, China. E-mail address: pjin@stu.edu.cn
***Postal address: School of Mathematics and Natural Sciences, University of Wuppertal, 42119 Wuppertal, Germany. E-mail address: kremer@math.uni-wuppertal.de
****Postal address: School of Mathematics and Natural Sciences, University of Wuppertal, 42119 Wuppertal, Germany. E-mail address: ruediger@uni-wuppertal.de
Get access Rights & Permissions [Opens in a new window]

Abstract

This article investigates the long-time behavior of conservative affine processes on the cone of symmetric positive semide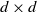finite $d\times d$ matrices. In particular, for conservative and subcritical affine processes we show that a finite 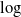$\log$ -moment of the state-independent jump measure is sufficient for the existence of a unique limit distribution. Moreover, we study the convergence rate of the underlying transition kernel to the limit distribution: first, in a specific metric induced by the Laplace transform, and second, in the Wasserstein distance under a first moment assumption imposed on the state-independent jump measure and an additional condition on the diffusion parameter.

Keywords

Affine processinvariant distributionlimit distributionergodicity

MSC classification

Primary: 60J25: Continuous-time Markov processes on general state spaces 37A25: Ergodicity, mixing, rates of mixing
Secondary: 60G10: Stationary processes 60J75: Jump processes
Type
Original Article
Information
Advances in Applied Probability , Volume 52 , Issue 3 , September 2020 , pp. 825 - 854
Check for updates
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfonsi, A., Kebaier, A. and Rey, C. (2016). Maximum likelihood estimation for Wishart processes. Stoch. Proc. Appl. 126, 3243–3282.CrossRefGoogle Scholar
Andersen, L. B. G. and Piterbarg, V. V. (2007). Moment explosions in stochastic volatility models. Finance Stoch. 11, 29–50.CrossRefGoogle Scholar
Baldeaux, J. and Platen, E. (2013). Functionals of Multidimensional Diffusions with Applications to Finance (Bocconi & Springer Series 5). Springer, Cham.Google Scholar
Barczy, M., Döring, L., Li, Z. and Pap, G. (2014). Stationarity and ergodicity for an affine two-factor model. Adv. Appl. Prob. 46, 878–898.CrossRefGoogle Scholar
Barczy, M., Li, Z. and Pap, G. (2015). Stochastic differential equation with jumps for multi-type continuous state and continuous time branching processes with immigration. Lat. Am. J. Prob. Math. Statist. 12, 129–169.Google Scholar
Barczy, M., Li, Z. and Pap, G. (2016). Moment formulas for multitype continuous state and continuous time branching process with immigration. J. Theoret. Prob. 29, 958–995.CrossRefGoogle Scholar
Barndorff-Nielsen, O. E. and Stelzer, R. (2007). Positive-definite matrix processes of finite variation. Prob. Math. Statist. 27, 3–43.Google Scholar
Behme, A., Lindner, A. and Maller, R. (2011). Stationary solutions of the stochastic differential equation $dV_t=V_{t^-}dU_t+dL_t$ with Lévy noise. Stoch. Proc. Appl. 121, 91–108.CrossRefGoogle Scholar
Biagini, F., Gnoatto, A. and Härtel, M. (2018). Long-term yield in an affine HJM framework on $S_d^+$ . Appl. Math. Optimization 77, 405–441.CrossRefGoogle Scholar
Bru, M.-F. (1991). Wishart processes. J. Theoret. Prob. 4, 725–751.CrossRefGoogle Scholar
Chiarella, C., Da Fonseca, J. and Grasselli, M.Pricing range notes within Wishart affine models. Insurance Math. Econom. 58, 193–203.CrossRefGoogle Scholar
Cuchiero, C., Filipović, D., Mayerhofer, E. and Teichmann, J. (2011). Affine processes on positive semidefinite matrices. Ann. Appl. Prob. 21, 397–463.CrossRefGoogle Scholar
Cuchiero, C., Keller-Ressel, M., Mayerhofer, E. and Teichmann, J. (2016). Affine processes on symmetric cones. J. Theoret. Prob. 29, 359–422.CrossRefGoogle Scholar
Da Fonseca, J., Grasselli, M. and Tebaldi, C. (2007). Option pricing when correlations are stochastic: an analytical framework. Rev. Derivatives Res. 10, 151–180.CrossRefGoogle Scholar
Dawson, D. A. and Li, Z. (2006). Skew convolution semigroups and affine Markov processes. Ann. Prob. 34, 1103–1142.CrossRefGoogle Scholar
Duffie, D., Filipović, D. and Schachermayer, W. (2003). Affine processes and applications in finance. Ann. Appl. Prob. 13, 984–1053.Google Scholar
Filipović, D. and Mayerhofer, E. (2009). Affine diffusion processes: theory and applications. In Advanced Financial Modelling, Walter de Gruyter, Berlin, pp. 125–164.Google Scholar
Friesen, M., Jin, P., Kremer, J. and Rüdiger, B. (2019). Exponential ergodicity for stochastic equations of nonnegative processes with jumps. Preprint. Available at https://arxiv.org/abs/1902.02833.Google Scholar
Friesen, M., Jin, P. and Rüdiger, B. (2019). Stochastic equation and exponential ergodicity in Wasserstein distances for affine processes. To appear in Ann. Appl. Prob. Preprint available at https://arxiv.org/abs/1901.05815.Google Scholar
Glasserman, P. and Kim, K.-K. (2010). Moment explosions and stationary distributions in affine diffusion models. Math. Finance 20, 1–33.CrossRefGoogle Scholar
Gnoatto, A. (2012). The Wishart short rate model. Internat. J. Theoret. Appl. Finance 15, 1–24.CrossRefGoogle Scholar
Gnoatto, A. and Grasselli, M. (2014). An affine multicurrency model with stochastic volatility and stochastic interest rates. SIAM J. Financial Math. 5, 493–531.CrossRefGoogle Scholar
Gourieroux, C. and Sufana, R. (2010). Derivative pricing with Wishart multivariate stochastic volatility. J. Business Econom. Statist. 28, 438–451.CrossRefGoogle Scholar
Gourieroux, C. and Sufana, R. (2011). Discrete time Wishart term structure models. J. Econom. Dynam. Control 35, 815–824.CrossRefGoogle Scholar
Grasselli, M. and Miglietta, G. (2016). A flexible spot multiple-curve model. Quant. Finance 16, 1465–1477.CrossRefGoogle Scholar
Heston, S. L. (1993). A closed-form solution for options with stochastic volatility with applications to bond and currency options. Rev. Financial Studies 6, 327–343.CrossRefGoogle Scholar
Horn, R. A. and Johnson, C. R. (2013). Matrix Analysis, 2nd edn. Cambridge University Press.Google Scholar
Jena, R. P., Kim, K.-K. and Xing, H. (2012). Long-term and blow-up behaviors of exponential moments in multi-dimensional affine diffusions. Stoch. Proc. Appl. 122, 2961–2993.CrossRefGoogle Scholar
Jin, P., Kremer, J. and Rüdiger, B. (2017). Exponential ergodicity of an affine two-factor model based on the $\alpha$ -root process. Adv. Appl. Prob. 49, 1144–1169.CrossRefGoogle Scholar
Jin, P., Kremer, J. and Rüdiger, B. (2020). Existence of limiting distribution for affine processes. J. Math. Anal. Appl. 486, 123912.CrossRefGoogle Scholar
Kawazu, K. and Watanabe, S. (1971). Branching processes with immigration and related limit theorems. Teor. Veroyat. Primen. 16, 34–51.Google Scholar
Keller-Ressel, M. (2011). Moment explosions and long-term behavior of affine stochastic volatility models. Math. Finance 21, 73–98.CrossRefGoogle Scholar
Keller-Ressel, M. and Mayerhofer, E. (2015). Exponential moments of affine processes. Ann. Appl. Prob. 25, 714–752.CrossRefGoogle Scholar
Keller-Ressel, M. and Mijatović, A. (2012). On the limit distributions of continuous-state branching processes with immigration. Stoch. Proc. Appl. 122, 2329–2345.CrossRefGoogle Scholar
Keller-Ressel, M., Schachermayer, W. and Teichmann, J. (2011). Affine processes are regular. Prob. Theory Rel. Fields 151, 591–611.CrossRefGoogle Scholar
Keller-Ressel, M. and Steiner, T. (2008). Yield curve shapes and the asymptotic short rate distribution in affine one-factor models. Finance Stoch. 12, 149–172.CrossRefGoogle Scholar
Kevei, P. (2018). Ergodic properties of generalized Ornstein–Uhlenbeck processes. Stoch. Proc. Appl. 128, 156–181.CrossRefGoogle Scholar
Leippold, M. and Trojani, F. (2010). Asset pricing with matrix jump diffusions. Working paper.CrossRefGoogle Scholar
Li, Z. (2011). Measure-Valued Branching Markov Processes. Springer, Heidelberg.CrossRefGoogle Scholar
Li, Z. and Ma, C. (2015). Asymptotic properties of estimators in a stable Cox–Ingersoll–Ross model. Stoch. Proc. Appl. 125, 3196–3233.CrossRefGoogle Scholar
Masuda, H. (2004). On multidimensional Ornstein–Uhlenbeck processes driven by a general Lévy process. Bernoulli 10, 97–120.CrossRefGoogle Scholar
Mayerhofer, E. (2012). Affine processes on positive semidefinite $d\times d$ matrices have jumps of finite variation in dimension $d>1$ . Stoch. Proc. Appl. 122, 3445–3459.CrossRef1$+.+Stoch.+Proc.+Appl.122,+3445–3459.>Google Scholar
Mayerhofer, E., Pfaffel, O. and Stelzer, R. (2011). On strong solutions for positive definite jump diffusions. Stoch. Proc. Appl. 121, 2072–2086.CrossRefGoogle Scholar
Mayerhofer, E., Stelzer, R. and Vestweber, J. (2020). Geometric ergodicity of affine processes on cones. Stoch. Proc. Appl. 130, 4141–4173.CrossRefGoogle Scholar
Pigorsch, C. and Stelzer, R. (2009). On the definition, stationary distribution and second order structure of positive semidefinite Ornstein–Uhlenbeck type processes. Bernoulli 15, 754–773.CrossRefGoogle Scholar
Pinsky, M. A. (1972). Limit theorems for continuous state branching processes with immigration. Bull. Amer. Math. Soc. 78, 242–244.CrossRefGoogle Scholar
Sato, K. and Yamazato, M. (1984). Operator-self-decomposable distributions as limit distributions of processes of Ornstein–Uhlenbeck type. Stoch. Proc. Appl. 17, 73–100.CrossRefGoogle Scholar
Villani, C. (2009). Optimal Transport: Old and New. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar