Stochastic Geometry and Statistical Applications
On spatial thinning-replacement processes based on Voronoi cells
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 293-306
-
- Article
-
- You have access
- Export citation
Intersection densities of nonstationary Poisson processes of hypersurfaces
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 307-317
-
- Article
-
- You have access
- Export citation
The Palm-duality for random subsets of d-dimensional grids
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 318-325
-
- Article
-
- You have access
- Export citation
Explicit laws of large numbers for random nearest-neighbour-type graphs
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 326-342
-
- Article
-
- You have access
- Export citation
General Applied Probability
On the time value of absolute ruin with debit interest
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 343-359
-
- Article
-
- You have access
- Export citation
Ruin probability with certain stationary stable claims generated by conservative flows
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 360-384
-
- Article
-
- You have access
- Export citation
Approximations for the Gerber-Shiu expected discounted penalty function in the compound poisson risk model
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 385-406
-
- Article
-
- You have access
- Export citation
Large deviation properties of constant rate data streams sharing a buffer with long-range dependent traffic in critical loading
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 407-428
-
- Article
-
- You have access
- Export citation
Zero-automatic queues and product form
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 429-461
-
- Article
-
- You have access
- Export citation
Stability of nonlinear stochastic recursions with application to nonlinear AR-GARCH models
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 462-491
-
- Article
-
- You have access
- Export citation
First-crossing and ballot-type results for some nonstationary sequences
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 492-509
-
- Article
-
- You have access
- Export citation
Optimal hitting time and perpetual option in a non-Lévy model: application to real options
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 510-530
-
- Article
-
- You have access
- Export citation
Inference in Lévy-type stochastic volatility models
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 531-549
-
- Article
-
- You have access
- Export citation
A weighted random walk model, with application to a genetic algorithm
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 550-568
-
- Article
-
- You have access
- Export citation
Markovian paths to extinction
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 569-587
-
- Article
-
- You have access
- Export citation
Random motions at finite velocity in a non-Euclidean space
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 588-611
-
- Article
-
- You have access
- Export citation
Front Matter
AAP volume 39 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Matter
AAP volume 39 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation



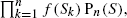 where the function
where the function