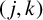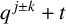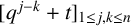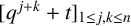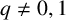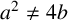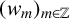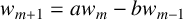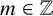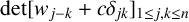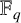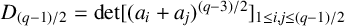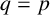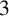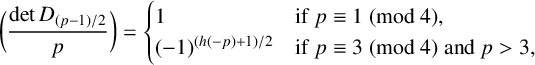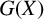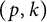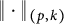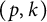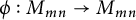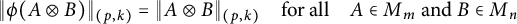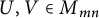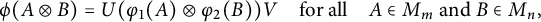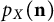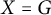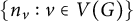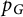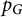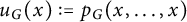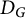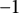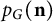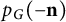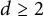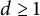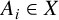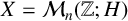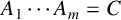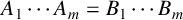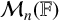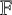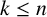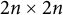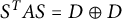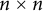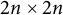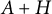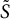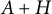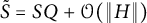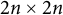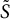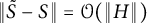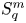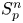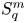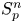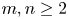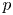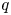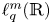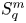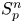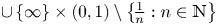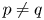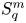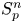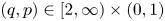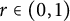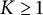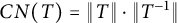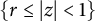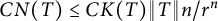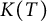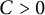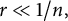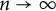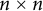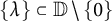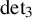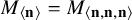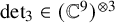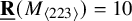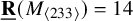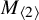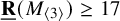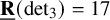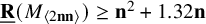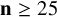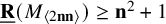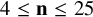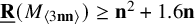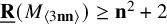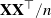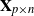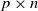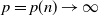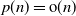184 results in 15Axx
CHARACTERISTIC POLYNOMIALS OF THE MATRICES WITH
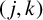 $(\,j,k)$-ENTRY
$(\,j,k)$-ENTRY 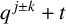 $q^{\,j\pm k}+t$
$q^{\,j\pm k}+t$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-10
-
- Article
- Export citation
A reproducing kernel approach to Lebesgue decomposition
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INVERSE CONNECTION FORMULAE FOR GENERALISED BESSEL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GENERALISED LEGENDRE MATRICES INVOLVING ROOTS OF UNITY OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-12
-
- Article
- Export citation
MAXIMAL SUBSEMIGROUPS OF INFINITE SYMMETRIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 29 January 2024, pp. 1-14
-
- Article
- Export citation
Linear maps preserving
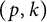 $(p,k)$-norms of tensor products of matrices
$(p,k)$-norms of tensor products of matrices
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 December 2023, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unified bounds for the independence number of graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 December 2023, pp. 1-21
-
- Article
- Export citation
The blowup-polynomial of a metric space: connections to stable polynomials, graphs and their distance spectra
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 November 2023, pp. 1-42
-
- Article
- Export citation
Norms on complex matrices induced by random vectors II: extension of weakly unitarily invariant norms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 447-457
- Print publication:
- June 2024
-
- Article
- Export citation
SOME COUNTING QUESTIONS FOR MATRIX PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 09 October 2023, pp. 1-12
-
- Article
- Export citation
ON EXTERIOR POWERS OF REFLECTION REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2023, pp. 1-13
-
- Article
- Export citation
Block perturbation of symplectic matrices in Williamson’s theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 201-214
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erdős–Ko–Rado theorem in Peisert-type graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 176-187
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On isometric embeddability of $S_q^m$
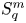 into $S_p^n$
into $S_p^n$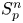 as non-commutative quasi-Banach spaces
as non-commutative quasi-Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 June 2023, pp. 1-24
-
- Article
- Export citation
LEFT AND RIGHT EIGENVECTORS OF A VARIANT OF THE SYLVESTER–KAC MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 316-326
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the condition number of a Kreiss matrix
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1376-1390
- Print publication:
- December 2023
-
- Article
- Export citation
New lower bounds for matrix multiplication and
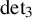 $\operatorname {det}_3$
$\operatorname {det}_3$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 29 May 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large deviations of extremal eigenvalues of sample covariance matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1275-1280
- Print publication:
- December 2023
-
- Article
- Export citation
A generalization of Kruskal’s theorem on tensor decomposition
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 April 2023, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subsymmetric exchanged braids and the Burau matrix
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 154-187
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation