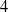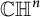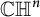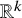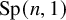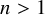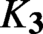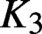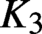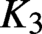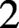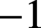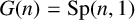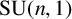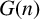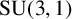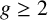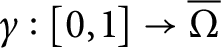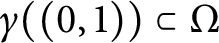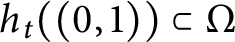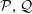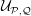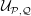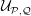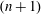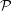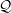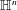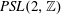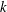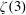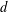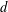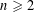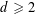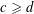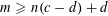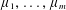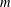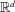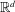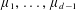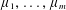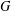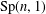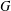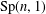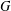48 results in 51Mxx
Examples of hyperbolic spaces without the properties of quasi-ball or bounded eccentricity
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-9
-
- Article
- Export citation
Joint partial equidistribution of Farey rays in negatively curved manifolds and trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 January 2024, pp. 1-37
-
- Article
- Export citation
Assembling RKHS with Pick kernels and assembling polyhedra in
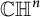 $\mathbb {CH} ^{n}$
$\mathbb {CH} ^{n}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A presentation for the Eisenstein-Picard modular group in three complex dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 25 July 2023, pp. 625-654
- Print publication:
- September 2023
-
- Article
- Export citation
ARITHMETICITY OF
 $\mathbb {C}$-FUCHSIAN SUBGROUPS OF SOME NONARITHMETIC LATTICES
$\mathbb {C}$-FUCHSIAN SUBGROUPS OF SOME NONARITHMETIC LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 77-88
- Print publication:
- February 2024
-
- Article
- Export citation
Families of similar simplices inscribed in most smoothly embedded spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 November 2022, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric versions of Schwarz’s lemma for spherically convex functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1780-1799
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quaternionic hyperbolic lattices of minimal covolume
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 25 August 2022, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sub-tree counts on hyperbolic random geometric graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 1032-1069
- Print publication:
- December 2022
-
- Article
- Export citation
Hyperbolic tessellations and generators of
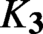 ${K}_{\textbf {3}}$ for imaginary quadratic fields
${K}_{\textbf {3}}$ for imaginary quadratic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 24 May 2021, e40
-
- Article
-
- You have access
- Open access
- Export citation
LOCAL COORDINATES FOR COMPLEX AND QUATERNIONIC HYPERBOLIC PAIRS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 57-78
- Print publication:
- August 2022
-
- Article
- Export citation
Shortest paths in arbitrary plane domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 09 November 2020, pp. 349-367
- Print publication:
- April 2022
-
- Article
- Export citation
Continuity of the SRB entropy of convex projective structures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 04 June 2020, pp. 2369-2381
- Print publication:
- August 2021
-
- Article
- Export citation
FRIEZE PATTERNS WITH COEFFICIENTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 March 2020, e17
-
- Article
-
- You have access
- Open access
- Export citation
Universal Alternating Semiregular Polytopes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 12 February 2020, pp. 572-595
- Print publication:
- April 2021
-
- Article
- Export citation
Ideal Uniform Polyhedra in
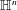 $\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
$\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 465-492
- Print publication:
- April 2021
-
- Article
- Export citation
SPLITTING LOOPS AND NECKLACES: VARIANTS OF THE SQUARE PEG PROBLEM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 January 2020, e5
-
- Article
-
- You have access
- Open access
- Export citation
CUTTING A PART FROM MANY MEASURES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 17 October 2019, e37
-
- Article
-
- You have access
- Open access
- Export citation
Equality case for an elliptic area condenser inequality and a related Schwarz type lemma
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 19 August 2019, pp. 91-104
-
- Article
- Export citation
ON DISCRETENESS OF SUBGROUPS OF QUATERNIONIC HYPERBOLIC ISOMETRIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 16 August 2019, pp. 283-293
- Print publication:
- April 2020
-
- Article
- Export citation