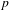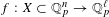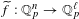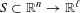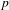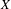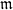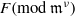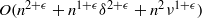27 results in 12Jxx
Hensel minimality II: Mixed characteristic and a diophantine application
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decidability of the class of all the rings
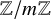 $\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
$\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOTES ON ATKIN–LEHNER THEORY FOR DRINFELD MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 50-68
- Print publication:
- August 2023
-
- Article
- Export citation
Cohomology of algebraic varieties over non-archimedean fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 October 2022, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the analyticity of WLUD∞ functions of one variable and WLUD∞ functions of several variables in a complete non-Archimedean valued field
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 07 July 2022, pp. 691-704
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting closed asymptotic couples
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 20 June 2022, pp. 530-555
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality I
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 May 2022, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEFINABILITY OF HENSELIAN VALUATIONS BY CONDITIONS ON THE VALUE GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 April 2022, pp. 1064-1082
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Model Theoretic Properties of O-minimal Exponential Fields
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 February 2022, pp. 529-530
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
Chaotic behavior of the p-adic Potts–Bethe mapping II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3433-3457
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SURREAL ORDERED EXPONENTIAL FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 1066-1115
- Print publication:
- September 2021
-
- Article
- Export citation
Transfer Principles in Henselian Valued Fields
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 222-223
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
A NOTE ON p-ADIC SIMPLICIAL VOLUMES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2020, pp. 563-583
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
DEFINABLE SETS OF BERKOVICH CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 11 October 2019, pp. 1275-1339
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation
Existence of valuations with smallest normalized volume
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 820-849
- Print publication:
- April 2018
-
- Article
-
- You have access
- HTML
- Export citation
Generalized Euler characteristic in power-bounded T-convex valued fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 14 September 2017, pp. 2591-2642
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
A Generalization of the Eisenstein–Dumas–Schönemann Irreducibility Criterion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 937-945
-
- Article
- Export citation
Defining Coarsenings of Valuations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 665-687
-
- Article
- Export citation
A DEFINABLE
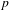 $p$-ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
$p$-ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 October 2015, pp. 39-57
- Print publication:
- February 2018
-
- Article
- Export citation
Complexity of OM factorizations of polynomials over local fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 June 2013, pp. 139-171
-
- Article
-
- You have access
- Export citation



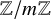
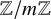
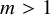
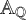

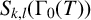
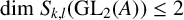
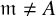
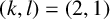
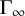

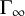
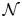
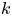
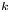
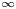
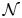
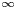
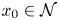
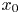
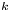
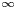
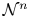
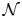
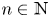
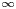
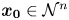
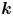
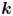
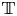
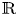
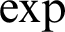
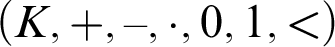
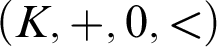
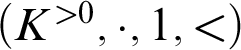
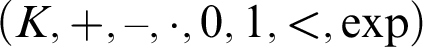
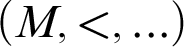
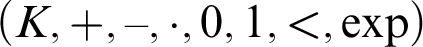
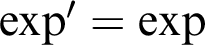
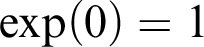
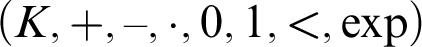
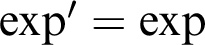

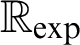
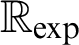
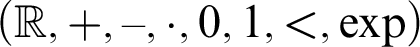
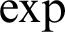
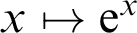
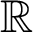
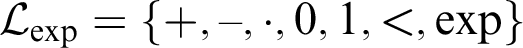
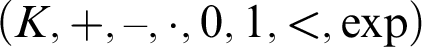
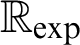
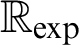
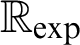
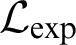
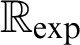
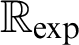
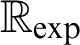
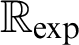
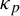
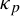


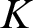
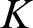

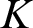


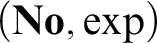
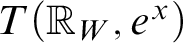
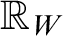


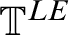

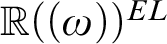
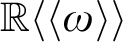

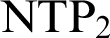
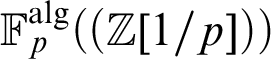
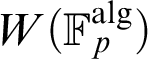
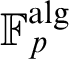

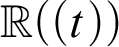
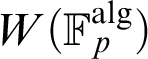

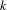
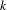
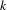
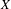
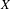
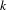
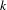

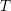
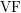
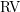
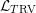
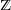
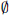 -definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.
-definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.