Published online by Cambridge University Press: 13 August 2021
In 2001, the algebraico-tree-theoretic simplicity hierarchical structure of J. H. Conway’s ordered field  ${\mathbf {No}}$
of surreal numbers was brought to the fore by the first author and employed to provide necessary and sufficient conditions for an ordered field (ordered
${\mathbf {No}}$
of surreal numbers was brought to the fore by the first author and employed to provide necessary and sufficient conditions for an ordered field (ordered 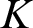 $K$
-vector space) to be isomorphic to an initial subfield (
$K$
-vector space) to be isomorphic to an initial subfield (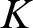 $K$
-subspace) of
$K$
-subspace) of  ${\mathbf {No}}$
, i.e. a subfield (
${\mathbf {No}}$
, i.e. a subfield (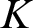 $K$
-subspace) of
$K$
-subspace) of  ${\mathbf {No}}$
that is an initial subtree of
${\mathbf {No}}$
that is an initial subtree of  ${\mathbf {No}}$
. In this sequel, analogous results are established for ordered exponential fields, making use of a slight generalization of Schmeling’s conception of a transseries field. It is further shown that a wide range of ordered exponential fields are isomorphic to initial exponential subfields of
${\mathbf {No}}$
. In this sequel, analogous results are established for ordered exponential fields, making use of a slight generalization of Schmeling’s conception of a transseries field. It is further shown that a wide range of ordered exponential fields are isomorphic to initial exponential subfields of 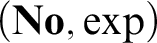 $({\mathbf {No}}, \exp )$
. These include all models of
$({\mathbf {No}}, \exp )$
. These include all models of 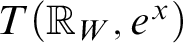 $T({\mathbb R}_W, e^x)$
, where
$T({\mathbb R}_W, e^x)$
, where 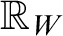 ${\mathbb R}_W$
is the reals expanded by a convergent Weierstrass system W. Of these, those we call trigonometric-exponential fields are given particular attention. It is shown that the exponential functions on the initial trigonometric-exponential subfields of
${\mathbb R}_W$
is the reals expanded by a convergent Weierstrass system W. Of these, those we call trigonometric-exponential fields are given particular attention. It is shown that the exponential functions on the initial trigonometric-exponential subfields of  ${\mathbf {No}}$
, which includes
${\mathbf {No}}$
, which includes  ${\mathbf {No}}$
itself, extend to canonical exponential functions on their surcomplex counterparts. The image of the canonical map of the ordered exponential field
${\mathbf {No}}$
itself, extend to canonical exponential functions on their surcomplex counterparts. The image of the canonical map of the ordered exponential field 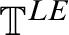 ${\mathbb T}^{LE}$
of logarithmic-exponential transseries into
${\mathbb T}^{LE}$
of logarithmic-exponential transseries into  ${\mathbf {No}}$
is shown to be initial, as are the ordered exponential fields
${\mathbf {No}}$
is shown to be initial, as are the ordered exponential fields 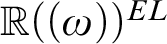 ${\mathbb R}((\omega ))^{EL}$
and
${\mathbb R}((\omega ))^{EL}$
and 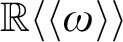 ${\mathbb R}\langle \langle \omega \rangle \rangle $
.
${\mathbb R}\langle \langle \omega \rangle \rangle $
.
The in-text reference citations have been corrected. An erratum detailing this update has also been published (doi: 10.1017/jsl.2022.5).
Please note a has been issued for this article.