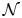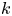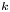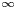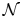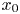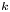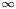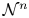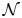1. Introduction
Let $\mathcal {N}$![]() be a non-Archimedean-ordered field extension of $ {\mathbb {R}}$
be a non-Archimedean-ordered field extension of $ {\mathbb {R}}$![]() that is real closed and complete in the order topology and whose Hahn group $S_\mathcal {N}$
that is real closed and complete in the order topology and whose Hahn group $S_\mathcal {N}$![]() is Archimedean, i.e. (isomorphic to) a subgroup of $ {\mathbb {R}}$
is Archimedean, i.e. (isomorphic to) a subgroup of $ {\mathbb {R}}$![]() . Recall that $S_{\mathcal {N}}$
. Recall that $S_{\mathcal {N}}$![]() is the set of equivalence classes under the relation $\sim$
is the set of equivalence classes under the relation $\sim$![]() defined on $\mathcal {N}^{*}:=\mathcal {N}{\setminus} \{0\}$
defined on $\mathcal {N}^{*}:=\mathcal {N}{\setminus} \{0\}$![]() as follows: For $x,\,y\in \mathcal {N}^{*}$
as follows: For $x,\,y\in \mathcal {N}^{*}$![]() , we say that $x$
, we say that $x$![]() is of the same order as $y$
is of the same order as $y$![]() and write $x\sim y$
and write $x\sim y$![]() if there exist $n,\,m\in {\mathbb {N}}$
if there exist $n,\,m\in {\mathbb {N}}$![]() such that $n|x|>|y|$
such that $n|x|>|y|$![]() and $m|y|>|x|$
and $m|y|>|x|$![]() , where $|\cdot |$
, where $|\cdot |$![]() denotes the ordinary absolute value on $\mathcal {N}$
denotes the ordinary absolute value on $\mathcal {N}$![]() : $|x|=\max \left \{x,\, -x\right \}$
: $|x|=\max \left \{x,\, -x\right \}$![]() . $S_{\mathcal {N}}$
. $S_{\mathcal {N}}$![]() is naturally endowed with an addition via $[x]+[y]=[x\cdot y]$
is naturally endowed with an addition via $[x]+[y]=[x\cdot y]$![]() and an order via $[x]<[y]$
and an order via $[x]<[y]$![]() if $|y|\ll |x|$
if $|y|\ll |x|$![]() (which means $n|y|< |x|$
(which means $n|y|< |x|$![]() for all $n\in \mathbb {N}$
for all $n\in \mathbb {N}$![]() ), both of which are readily checked to be well defined. It follows that $(S_{\mathcal {N}},\,+,\,<)$
), both of which are readily checked to be well defined. It follows that $(S_{\mathcal {N}},\,+,\,<)$![]() is an ordered group, often referred to as the Hahn group or skeleton group, whose neutral element is $[1]$
is an ordered group, often referred to as the Hahn group or skeleton group, whose neutral element is $[1]$![]() , the class of $1$
, the class of $1$![]() .
.
The theorem of Hahn [Reference Hahn3] provides a complete classification of non-Archimedean-ordered field extensions of $ {\mathbb {R}}$![]() in terms of their skeleton groups. In fact, invoking the axiom of choice, it is shown that the elements of our field $\mathcal {N}$
in terms of their skeleton groups. In fact, invoking the axiom of choice, it is shown that the elements of our field $\mathcal {N}$![]() can be written as (generalized) formal power series (also called Hahn series) over its skeleton group $S_{\mathcal {N}}$
can be written as (generalized) formal power series (also called Hahn series) over its skeleton group $S_{\mathcal {N}}$![]() with real coefficients, and the set of appearing exponents forms a well-ordered subset of $S_{\mathcal {N}}$
with real coefficients, and the set of appearing exponents forms a well-ordered subset of $S_{\mathcal {N}}$![]() . That is, for all $x\in \mathcal {N}$
. That is, for all $x\in \mathcal {N}$![]() , we have that $x=\sum \nolimits _{q\in S_{\mathcal {N}}}a_qd^{q}$
, we have that $x=\sum \nolimits _{q\in S_{\mathcal {N}}}a_qd^{q}$![]() ; with $a_q\in {\mathbb {R}}$
; with $a_q\in {\mathbb {R}}$![]() for all $q$
for all $q$![]() , $d$
, $d$![]() a positive infinitely small element of $\mathcal {N}$
a positive infinitely small element of $\mathcal {N}$![]() , and the support of $x$
, and the support of $x$![]() , given by $\mbox {supp}(x):=\{q\in S_\mathcal {N}: a_q\ne 0\}$
, given by $\mbox {supp}(x):=\{q\in S_\mathcal {N}: a_q\ne 0\}$![]() , forming a well-ordered subset of $S_{\mathcal {N}}$
, forming a well-ordered subset of $S_{\mathcal {N}}$![]() .
.
We define for $x\ne 0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() , $\lambda (x)=\min (\mbox {supp}(x))$
, $\lambda (x)=\min (\mbox {supp}(x))$![]() , which exists since $\mbox {supp}(x)$
, which exists since $\mbox {supp}(x)$![]() is well ordered. Moreover, we set $\lambda (0)=\infty$
is well ordered. Moreover, we set $\lambda (0)=\infty$![]() . Given a non-zero $x=\sum \nolimits _{q\in \mbox {supp}(x)}a_qd^{q}$
. Given a non-zero $x=\sum \nolimits _{q\in \mbox {supp}(x)}a_qd^{q}$![]() , then $x>0$
, then $x>0$![]() if and only if $a_{\lambda (x)}>0$
if and only if $a_{\lambda (x)}>0$![]() .
.
The smallest such field $\mathcal {N}$![]() is the Levi-Civita field $\mathcal {R}$
is the Levi-Civita field $\mathcal {R}$![]() , first introduced in [Reference Levi-Civita5, Reference Levi-Civita6]. In this case, $S_\mathcal {R}= {\mathbb {Q}}$
, first introduced in [Reference Levi-Civita5, Reference Levi-Civita6]. In this case, $S_\mathcal {R}= {\mathbb {Q}}$![]() , and for any element $x\in \mathcal {R}$
, and for any element $x\in \mathcal {R}$![]() , supp$(x)$
, supp$(x)$![]() is a left-finite subset of $ {\mathbb {Q}}$
is a left-finite subset of $ {\mathbb {Q}}$![]() , i.e. below any rational bound $r$
, i.e. below any rational bound $r$![]() there are only finitely many exponents in the Hahn representation of $x$
there are only finitely many exponents in the Hahn representation of $x$![]() . The Levi-Civita field $\mathcal {R}$
. The Levi-Civita field $\mathcal {R}$![]() is of particular interest because of its practical usefulness. Since the supports of the elements of $\mathcal {R}$
is of particular interest because of its practical usefulness. Since the supports of the elements of $\mathcal {R}$![]() are left-finite, it is possible to represent these numbers on a computer. Having infinitely small numbers allows for many computational applications; one such application is the computation of derivatives of real functions representable on a computer [Reference Shamseddine and Berz13, Reference Shamseddine and Berz15], where both the accuracy of formula manipulators and the speed of classical numerical methods are achieved. For a review of the Levi-Civita field $\mathcal {R}$
are left-finite, it is possible to represent these numbers on a computer. Having infinitely small numbers allows for many computational applications; one such application is the computation of derivatives of real functions representable on a computer [Reference Shamseddine and Berz13, Reference Shamseddine and Berz15], where both the accuracy of formula manipulators and the speed of classical numerical methods are achieved. For a review of the Levi-Civita field $\mathcal {R}$![]() , see [Reference Shamseddine11] and references therein.
, see [Reference Shamseddine11] and references therein.
In the wider context of valuation theory, it is interesting to note that the topology induced by the order on $\mathcal {N}$![]() is the same as the valuation topology $\tau _v$
is the same as the valuation topology $\tau _v$![]() introduced via the non-Archimedean (ultrametric) valuation $|\cdot |_v:\mathcal {N}\rightarrow \mathbb {R}$
introduced via the non-Archimedean (ultrametric) valuation $|\cdot |_v:\mathcal {N}\rightarrow \mathbb {R}$![]() , given by
, given by
It follows, therefore, that the field $\mathcal {N}$![]() is just a special case of the class of fields discussed in [Reference Schikhof9]. For a general overview of the algebraic properties of formal power series fields, we refer to the comprehensive overview by Ribenboim [Reference Ribenboim8], and for an overview of the related valuation theory the book by Krull [Reference Krull4]. A thorough and complete treatment of ordered structures can also be found in [Reference Priess-Crampe7]. A more comprehensive survey of all non-Archimedean fields can be found in [Reference Barría Comicheo and Shamseddine1].
is just a special case of the class of fields discussed in [Reference Schikhof9]. For a general overview of the algebraic properties of formal power series fields, we refer to the comprehensive overview by Ribenboim [Reference Ribenboim8], and for an overview of the related valuation theory the book by Krull [Reference Krull4]. A thorough and complete treatment of ordered structures can also be found in [Reference Priess-Crampe7]. A more comprehensive survey of all non-Archimedean fields can be found in [Reference Barría Comicheo and Shamseddine1].
2. Weak local uniform differentiability and review of recent results
Because of the total disconnectedness of the field $\mathcal {N}$![]() in the order topology, the standard theorems of real calculus like the intermediate value theorem, the inverse function theorem, the mean value theorem, the implicit function theorem and Taylor's theorem require stronger smoothness criteria of the functions involved in order for the theorems to hold. In this section, we will present one such criterion: the so-called weak local uniform differentiability, we will review recent work based on that smoothness criterion and then present new results.
in the order topology, the standard theorems of real calculus like the intermediate value theorem, the inverse function theorem, the mean value theorem, the implicit function theorem and Taylor's theorem require stronger smoothness criteria of the functions involved in order for the theorems to hold. In this section, we will present one such criterion: the so-called weak local uniform differentiability, we will review recent work based on that smoothness criterion and then present new results.
In [Reference Bookatz and Shamseddine2], we focus our attention on $\mathcal {N}$![]() -valued functions of one variable. We study the properties of weakly locally uniformly differentiable (WLUD) functions at a point $x_0\in \mathcal {N}$
-valued functions of one variable. We study the properties of weakly locally uniformly differentiable (WLUD) functions at a point $x_0\in \mathcal {N}$![]() or on an open subset $A$
or on an open subset $A$![]() of $\mathcal {N}$
of $\mathcal {N}$![]() . In particular, we show that WLUD functions are $C^{1}$
. In particular, we show that WLUD functions are $C^{1}$![]() , they include all polynomial functions, and they are closed under addition, multiplication and composition. Then, we generalize the definition of weak local uniform differentiability to any order. In particular, we study the properties of WLUD$^{2}$
, they include all polynomial functions, and they are closed under addition, multiplication and composition. Then, we generalize the definition of weak local uniform differentiability to any order. In particular, we study the properties of WLUD$^{2}$![]() functions at a point $x_0\in \mathcal {N}$
functions at a point $x_0\in \mathcal {N}$![]() or on an open subset $A$
or on an open subset $A$![]() of $\mathcal {N}$
of $\mathcal {N}$![]() ; and we show that WLUD$^{2}$
; and we show that WLUD$^{2}$![]() functions are $C^{2}$
functions are $C^{2}$![]() , they include all polynomial functions, and they are closed under addition, multiplication and composition. Finally, we formulate and prove an inverse function theorem as well as a local intermediate value theorem and a local mean value theorem for these functions.
, they include all polynomial functions, and they are closed under addition, multiplication and composition. Finally, we formulate and prove an inverse function theorem as well as a local intermediate value theorem and a local mean value theorem for these functions.
Here, we only recall the main definitions and results (without proofs) in [Reference Bookatz and Shamseddine2] and refer the reader to that paper for the details.
Definition 1 Let $A\subseteq \mathcal {N}$![]() be open, let $f:A\rightarrow \mathcal {N}$
be open, let $f:A\rightarrow \mathcal {N}$![]() , and let $x_0\in A$
, and let $x_0\in A$![]() be given. We say that $f$
be given. We say that $f$![]() is WLUD at $x_0$
is WLUD at $x_0$![]() if $f$
if $f$![]() is differentiable in a neighbourhood $\Omega$
is differentiable in a neighbourhood $\Omega$![]() of $x_0$
of $x_0$![]() in $A$
in $A$![]() and if for every $\epsilon > 0$
and if for every $\epsilon > 0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() there exists $\delta > 0$
there exists $\delta > 0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() such that $(x_0 - \delta,\, x_0 + \delta ) \subset \Omega$
such that $(x_0 - \delta,\, x_0 + \delta ) \subset \Omega$![]() , and for every $x,\,y \in (x_0 - \delta,\, x_0 + \delta )$
, and for every $x,\,y \in (x_0 - \delta,\, x_0 + \delta )$![]() we have that $\left \lvert {f(y) - f(x) - f^{\prime } (x)(y-x)}\right \rvert \le \epsilon \left \lvert {y-x}\right \rvert$
we have that $\left \lvert {f(y) - f(x) - f^{\prime } (x)(y-x)}\right \rvert \le \epsilon \left \lvert {y-x}\right \rvert$![]() . Moreover, we say that $f$
. Moreover, we say that $f$![]() is WLUD on $A$
is WLUD on $A$![]() if $f$
if $f$![]() is WLUD at every point in $A$
is WLUD at every point in $A$![]() .
.
We extend the WLUD concept to higher orders of differentiability and we define WLUD$^{k}$![]() as follows.
as follows.
Definition 2 Let $A\subseteq \mathcal {N}$![]() be open, let $f:A\rightarrow \mathcal {N}$
be open, let $f:A\rightarrow \mathcal {N}$![]() , let $x_0\in A$
, let $x_0\in A$![]() , and let $k\in \mathbb {N}$
, and let $k\in \mathbb {N}$![]() be given. We say that $f$
be given. We say that $f$![]() is WLUD$^{k}$
is WLUD$^{k}$![]() at $x_0$
at $x_0$![]() if $f$
if $f$![]() is $k$
is $k$![]() times differentiable in a neighbourhood $\Omega$
times differentiable in a neighbourhood $\Omega$![]() of $x_0$
of $x_0$![]() in $A$
in $A$![]() and if for every $\epsilon > 0$
and if for every $\epsilon > 0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() there exists $\delta > 0$
there exists $\delta > 0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() such that $(x_0-\delta,\,x_0+\delta ) \subset \Omega$
such that $(x_0-\delta,\,x_0+\delta ) \subset \Omega$![]() , and for every $x,\,y \in (x_0-\delta,\,x_0+\delta )$
, and for every $x,\,y \in (x_0-\delta,\,x_0+\delta )$![]() we have that
we have that

Moreover, we say that $f$![]() is WLUD$^{k}$
is WLUD$^{k}$![]() on $A$
on $A$![]() if $f$
if $f$![]() is WLUD$^{k}$
is WLUD$^{k}$![]() at every point in $A$
at every point in $A$![]() . Finally, we say that $f$
. Finally, we say that $f$![]() is WLUD$^{\infty }$
is WLUD$^{\infty }$![]() at $x_0$
at $x_0$![]() (respectively, on $A$
(respectively, on $A$![]() ) if $f$
) if $f$![]() is WLUD$^{k}$
is WLUD$^{k}$![]() at $x_0$
at $x_0$![]() (respectively, on $A$
(respectively, on $A$![]() ) for every $k\in \mathbb {N}$
) for every $k\in \mathbb {N}$![]() .
.
Theorem 1 Inverse Function Theorem
Let $A\subseteq \mathcal {N}$![]() be open, let $f:A\rightarrow \mathcal {N}$
be open, let $f:A\rightarrow \mathcal {N}$![]() be WLUD on $A,$
be WLUD on $A,$![]() and let $x_0 \in A$
and let $x_0 \in A$![]() be such that $f^{\prime }(x_0) \neq 0$
be such that $f^{\prime }(x_0) \neq 0$![]() . Then, there exists a neighbourhood $\Omega$
. Then, there exists a neighbourhood $\Omega$![]() of $x_0$
of $x_0$![]() in $A$
in $A$![]() such that
such that
(1) $\left.f\right |_\Omega$
 is one-to-one;
is one-to-one;(2) $f(\Omega )$
 is open and
is open and(3) $f^{-1}$
 exists and is WLUD on $f(\Omega )$
exists and is WLUD on $f(\Omega )$ with $(f^{-1})^{\prime } = 1/(f^{\prime } \circ f^{-1})$
with $(f^{-1})^{\prime } = 1/(f^{\prime } \circ f^{-1})$ .
.
Theorem 2 Local Intermediate Value Theorem
Let $A\subseteq \mathcal {N}$![]() be open, let $f:A\rightarrow \mathcal {N}$
be open, let $f:A\rightarrow \mathcal {N}$![]() be WLUD on $A,$
be WLUD on $A,$![]() and let $x_0 \in A$
and let $x_0 \in A$![]() be such that $f^{\prime }(x_0) \neq 0$
be such that $f^{\prime }(x_0) \neq 0$![]() . Then, there exists a neighbourhood $\Omega$
. Then, there exists a neighbourhood $\Omega$![]() of $x_0$
of $x_0$![]() in $A$
in $A$![]() such that for any $a< b$
such that for any $a< b$![]() in $f(\Omega )$
in $f(\Omega )$![]() and for any $c\in (a,\,b)$
and for any $c\in (a,\,b)$![]() , there is an $x\in (\min \left \{f^{(-1)}(a),\,f^{(-1)}(b)\right \},\,\max \left \{f^{(-1)}(a),\,f^{(-1)}(b)\right \})$
, there is an $x\in (\min \left \{f^{(-1)}(a),\,f^{(-1)}(b)\right \},\,\max \left \{f^{(-1)}(a),\,f^{(-1)}(b)\right \})$![]() such that $f(x)=c$
such that $f(x)=c$![]() .
.
Theorem 3 Local Mean Value Theorem
Let $A\subseteq \mathcal {N}$![]() be open, let $f:A\rightarrow \mathcal {N}$
be open, let $f:A\rightarrow \mathcal {N}$![]() be WLUD$^{2}$
be WLUD$^{2}$![]() on $A,$
on $A,$![]() and let $x_0 \in A$
and let $x_0 \in A$![]() be such that $f^{\prime \prime }(x_0) \neq 0$
be such that $f^{\prime \prime }(x_0) \neq 0$![]() . Then, there exists a neighbourhood $\Omega$
. Then, there exists a neighbourhood $\Omega$![]() of $x_0$
of $x_0$![]() in $A$
in $A$![]() such that $f$
such that $f$![]() has the mean value property on $\Omega$
has the mean value property on $\Omega$![]() . That is, for every $a,\,b\in \Omega$
. That is, for every $a,\,b\in \Omega$![]() with $a< b,$
with $a< b,$![]() there exists $c\in (a,\,b)$
there exists $c\in (a,\,b)$![]() such that
such that
In [Reference Shamseddine12], we formulate and prove a Taylor theorem with remainder for WLUD$^{k}$![]() functions from $\mathcal {N}$
functions from $\mathcal {N}$![]() to $\mathcal {N}$
to $\mathcal {N}$![]() . Then, we extend the concept of WLUD to functions from $\mathcal {N}^{n}$
. Then, we extend the concept of WLUD to functions from $\mathcal {N}^{n}$![]() to $\mathcal {N}^{m}$
to $\mathcal {N}^{m}$![]() with $m,\,n\in \mathbb {N}$
with $m,\,n\in \mathbb {N}$![]() and study the properties of those functions as we did for functions from $\mathcal {N}$
and study the properties of those functions as we did for functions from $\mathcal {N}$![]() to $\mathcal {N}$
to $\mathcal {N}$![]() . Then, we formulate and prove the inverse function theorem for WLUD functions from $\mathcal {N}^{n}$
. Then, we formulate and prove the inverse function theorem for WLUD functions from $\mathcal {N}^{n}$![]() to $\mathcal {N}^{n}$
to $\mathcal {N}^{n}$![]() and the implicit function theorem for WLUD functions from $\mathcal {N}^{n}$
and the implicit function theorem for WLUD functions from $\mathcal {N}^{n}$![]() to $\mathcal {N}^{m}$
to $\mathcal {N}^{m}$![]() with $m< n$
with $m< n$![]() in $\mathbb {N}$
in $\mathbb {N}$![]() .
.
As in the real case, the proof of Taylor's theorem with remainder uses the mean value theorem. However, in the non-Archimedean setting, stronger conditions on the function are needed than in the real case for the formulation of the theorem.
Theorem 5 Taylor's Theorem with Remainder
Let $A \subseteq \mathcal {N}$![]() be open, let $k\in \mathbb {N}$
be open, let $k\in \mathbb {N}$![]() be given, and let $f : A \rightarrow \mathcal {N}$
be given, and let $f : A \rightarrow \mathcal {N}$![]() be WLUD$^{k+2}$
be WLUD$^{k+2}$![]() on $A$
on $A$![]() . Assume further that $f^{(j)}$
. Assume further that $f^{(j)}$![]() is WLUD$^{2}$
is WLUD$^{2}$![]() on $A$
on $A$![]() for $0\leq j \leq k$
for $0\leq j \leq k$![]() . Then, for every $x\in A,$
. Then, for every $x\in A,$![]() there exists a neighbourhood $U$
there exists a neighbourhood $U$![]() of $x$
of $x$![]() in $A$
in $A$![]() such that, for any $y \in U$
such that, for any $y \in U$![]() , there exists $c \in [ \min \{y,\, x\},\,\max \{y,\, x\} ]$
, there exists $c \in [ \min \{y,\, x\},\,\max \{y,\, x\} ]$![]() such that
such that

Before we define weak local uniform differentiability for functions from $\mathcal {N}^{n}$![]() to $\mathcal {N}^{m}$
to $\mathcal {N}^{m}$![]() and then state the inverse function theorem and the implicit function theorem, we introduce the following notation.
and then state the inverse function theorem and the implicit function theorem, we introduce the following notation.
Notation 1 Let $A\subset \mathcal {N}^{n}$![]() be open, let $\boldsymbol {x_0}\in A$
be open, let $\boldsymbol {x_0}\in A$![]() be given, and let $\boldsymbol {f}:A\rightarrow \mathcal {N}^{m}$
be given, and let $\boldsymbol {f}:A\rightarrow \mathcal {N}^{m}$![]() be such that all the first-order partial derivatives of $\boldsymbol {f}$
be such that all the first-order partial derivatives of $\boldsymbol {f}$![]() at $\boldsymbol {x_0}$
at $\boldsymbol {x_0}$![]() exist. Then, $\boldsymbol {D}\boldsymbol {f}(\boldsymbol {x_0})$
exist. Then, $\boldsymbol {D}\boldsymbol {f}(\boldsymbol {x_0})$![]() denotes the linear map from $\mathcal {N}^{n}$
denotes the linear map from $\mathcal {N}^{n}$![]() to $\mathcal {N}^{m}$
to $\mathcal {N}^{m}$![]() defined by the $m\times n$
defined by the $m\times n$![]() Jacobian matrix of $\boldsymbol {f}$
Jacobian matrix of $\boldsymbol {f}$![]() at $\boldsymbol {x_0}$
at $\boldsymbol {x_0}$![]() :
:

with $\boldsymbol {f}^{i}_j(\boldsymbol {x_0})=\frac {\partial f_i}{\partial x_j}(\boldsymbol {x_0})$![]() for $1\le i\le m$
for $1\le i\le m$![]() and $1\le j\le n$
and $1\le j\le n$![]() . Moreover, if $m=n$
. Moreover, if $m=n$![]() then the determinant of the $n\times n$
then the determinant of the $n\times n$![]() matrix $\boldsymbol {D}\boldsymbol {f}(\boldsymbol {x_0})$
matrix $\boldsymbol {D}\boldsymbol {f}(\boldsymbol {x_0})$![]() is denoted by $J\boldsymbol {f}(\boldsymbol {x_0})$
is denoted by $J\boldsymbol {f}(\boldsymbol {x_0})$![]() .
.
Definition 3 WLUD
Let $A\subset \mathcal {N}^{n}$![]() be open, let $\boldsymbol {f}:A \to \mathcal {N}^{m}$
be open, let $\boldsymbol {f}:A \to \mathcal {N}^{m}$![]() , and let $\boldsymbol {x_0}\in A$
, and let $\boldsymbol {x_0}\in A$![]() be given. Then, we say that $\boldsymbol {f}$
be given. Then, we say that $\boldsymbol {f}$![]() is WLUD at $\boldsymbol {x_0}$
is WLUD at $\boldsymbol {x_0}$![]() if $\boldsymbol {f}$
if $\boldsymbol {f}$![]() is differentiable in a neighbourhood $\Omega$
is differentiable in a neighbourhood $\Omega$![]() of $\boldsymbol {x_0}$
of $\boldsymbol {x_0}$![]() in $A$
in $A$![]() and if for every $\epsilon >0$
and if for every $\epsilon >0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() there exists $\delta >0$
there exists $\delta >0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() such that $B_{\delta }(\boldsymbol {x_0}):=\left \{\boldsymbol {t}\in \mathcal {N}:\left |\boldsymbol {t}-\boldsymbol {x_0}\right |<\delta \right \}\subset \Omega$
such that $B_{\delta }(\boldsymbol {x_0}):=\left \{\boldsymbol {t}\in \mathcal {N}:\left |\boldsymbol {t}-\boldsymbol {x_0}\right |<\delta \right \}\subset \Omega$![]() , and for all $\boldsymbol {x},\,\boldsymbol {y}\in B_{\delta }(\boldsymbol {x_0})$
, and for all $\boldsymbol {x},\,\boldsymbol {y}\in B_{\delta }(\boldsymbol {x_0})$![]() we have that
we have that
Moreover, we say that $\boldsymbol {f}$![]() is WLUD on $A$
is WLUD on $A$![]() if $\boldsymbol {f}$
if $\boldsymbol {f}$![]() is WLUD at every point in $A$
is WLUD at every point in $A$![]() .
.
We show in [Reference Shamseddine12] that if $\boldsymbol {f}$![]() is WLUD at $\boldsymbol {x_0}$
is WLUD at $\boldsymbol {x_0}$![]() (respectively on $A$
(respectively on $A$![]() ) then $\boldsymbol {f}$
) then $\boldsymbol {f}$![]() is C$^{1}$
is C$^{1}$![]() at $\boldsymbol {x_0}$
at $\boldsymbol {x_0}$![]() (respectively, on $A$
(respectively, on $A$![]() ). Thus, the class of WLUD functions at a point $\boldsymbol {x_0}$
). Thus, the class of WLUD functions at a point $\boldsymbol {x_0}$![]() (respectively, on an open set $A$
(respectively, on an open set $A$![]() ) is a subset of the class of $C^{1}$
) is a subset of the class of $C^{1}$![]() functions at $\boldsymbol {x_0}$
functions at $\boldsymbol {x_0}$![]() (respectively, on $A$
(respectively, on $A$![]() ). However, this is still large enough to include all polynomial functions. We also show in [Reference Shamseddine12] that if $\boldsymbol {f},\,\boldsymbol {g}$
). However, this is still large enough to include all polynomial functions. We also show in [Reference Shamseddine12] that if $\boldsymbol {f},\,\boldsymbol {g}$![]() are WLUD at $\boldsymbol {x_0}$
are WLUD at $\boldsymbol {x_0}$![]() (respectively, on $A$
(respectively, on $A$![]() ) and if $\alpha \in \mathcal {N}$
) and if $\alpha \in \mathcal {N}$![]() then $\boldsymbol {f}+\alpha \boldsymbol {g}$
then $\boldsymbol {f}+\alpha \boldsymbol {g}$![]() and $\boldsymbol {f}\cdot \boldsymbol {g}$
and $\boldsymbol {f}\cdot \boldsymbol {g}$![]() are WLUD at $\boldsymbol {x_0}$
are WLUD at $\boldsymbol {x_0}$![]() (respectively, on $A$
(respectively, on $A$![]() ). Moreover, we show that if $\boldsymbol {f}:A \to \mathcal {N}^{m}$
). Moreover, we show that if $\boldsymbol {f}:A \to \mathcal {N}^{m}$![]() is WLUD at $\boldsymbol {x_0}\in A$
is WLUD at $\boldsymbol {x_0}\in A$![]() (respectively, on $A$
(respectively, on $A$![]() ) and if $\boldsymbol {g}:C \to \mathcal {N}^{p}$
) and if $\boldsymbol {g}:C \to \mathcal {N}^{p}$![]() is WLUD at $\boldsymbol {f}(\boldsymbol {x_0})\in C$
is WLUD at $\boldsymbol {f}(\boldsymbol {x_0})\in C$![]() (respectively, on $C$
(respectively, on $C$![]() ), where $A$
), where $A$![]() is an open subset of $\mathcal {N}^{n}$
is an open subset of $\mathcal {N}^{n}$![]() , $C$
, $C$![]() an open subset of $\mathcal {N}^{m}$
an open subset of $\mathcal {N}^{m}$![]() and $\boldsymbol {f}(A) \subseteq C$
and $\boldsymbol {f}(A) \subseteq C$![]() , then $\boldsymbol {g} \circ \boldsymbol {f}$
, then $\boldsymbol {g} \circ \boldsymbol {f}$![]() is WLUD at $\boldsymbol {x_0}$
is WLUD at $\boldsymbol {x_0}$![]() (respectively, on $A$
(respectively, on $A$![]() ).
).
Theorem 6 Inverse Function Theorem
Let $A\subset \mathcal {N}^{n}$![]() be open, let $\boldsymbol {f}:A\rightarrow \mathcal {N}^{n}$
be open, let $\boldsymbol {f}:A\rightarrow \mathcal {N}^{n}$![]() be WLUD on $A$
be WLUD on $A$![]() and let $\boldsymbol {t_0}\in A$
and let $\boldsymbol {t_0}\in A$![]() be such that $J\boldsymbol {f}(\boldsymbol {t_0})\neq 0$
be such that $J\boldsymbol {f}(\boldsymbol {t_0})\neq 0$![]() . Then, there is a neighbourhood $\Omega$
. Then, there is a neighbourhood $\Omega$![]() of $\boldsymbol {t_0}$
of $\boldsymbol {t_0}$![]() such that:
such that:
(1) $\boldsymbol {f}|_\Omega$
 is one-to-one;
is one-to-one;(2) $\boldsymbol {f}(\Omega )$
 is open and
is open and(3) the inverse $\boldsymbol {g}$
 of $\boldsymbol {f}|_\Omega$
of $\boldsymbol {f}|_\Omega$ is WLUD on $\boldsymbol {f}(\Omega )$
is WLUD on $\boldsymbol {f}(\Omega )$ ; and $\boldsymbol {D}\boldsymbol {g}(\boldsymbol {x})=[\boldsymbol {D}\boldsymbol {f}(\boldsymbol {t})]^{-1}$
; and $\boldsymbol {D}\boldsymbol {g}(\boldsymbol {x})=[\boldsymbol {D}\boldsymbol {f}(\boldsymbol {t})]^{-1}$ for $\boldsymbol {t}\in \Omega$
for $\boldsymbol {t}\in \Omega$ and $\boldsymbol {x}=\boldsymbol {f}(\boldsymbol {t})$
and $\boldsymbol {x}=\boldsymbol {f}(\boldsymbol {t})$ .
.
As in the real case, the inverse function theorem is used to prove the implicit function theorem. But before we state the implicit function theorem, we introduce the following notation.
Notation 2 Let $A\subseteq \mathcal {N}^{n}$![]() be open and let $\boldsymbol {\Phi }: A\rightarrow \mathcal {N}^{m}$
be open and let $\boldsymbol {\Phi }: A\rightarrow \mathcal {N}^{m}$![]() be WLUD on $A$
be WLUD on $A$![]() . For $\boldsymbol {t}=(t_1,\,...,\,t_{n-m},\,t_{n-m+1},\,...,\,t_{n} )\in A$
. For $\boldsymbol {t}=(t_1,\,...,\,t_{n-m},\,t_{n-m+1},\,...,\,t_{n} )\in A$![]() , let
, let
Theorem 7 Implicit Function Theorem
Let $\boldsymbol {\Phi }:A\rightarrow \mathcal {N}^{m}$![]() be WLUD on $A,$
be WLUD on $A,$![]() where $A\subseteq \mathcal {N}^{n}$
where $A\subseteq \mathcal {N}^{n}$![]() is open and $1\leq m< n.$
is open and $1\leq m< n.$![]() Let $\boldsymbol {t_0}\in A$
Let $\boldsymbol {t_0}\in A$![]() be such that $\boldsymbol {\Phi }(\boldsymbol {t_0})=\boldsymbol {0}$
be such that $\boldsymbol {\Phi }(\boldsymbol {t_0})=\boldsymbol {0}$![]() and ${\tilde {J}\boldsymbol {\Phi }(\boldsymbol {t_0})\neq 0}$
and ${\tilde {J}\boldsymbol {\Phi }(\boldsymbol {t_0})\neq 0}$![]() . Then, there exist a neighbourhood $U$
. Then, there exist a neighbourhood $U$![]() of $\boldsymbol {t_0}$
of $\boldsymbol {t_0}$![]() , a neighbourhood $R$
, a neighbourhood $R$![]() of $\hat {\boldsymbol {t_0}}$
of $\hat {\boldsymbol {t_0}}$![]() and $\boldsymbol {\phi }:R\rightarrow \mathcal {N}^{m}$
and $\boldsymbol {\phi }:R\rightarrow \mathcal {N}^{m}$![]() that is WLUD on $R$
that is WLUD on $R$![]() such that
such that
and
3. New results
This paper is a continuation of the work done in [Reference Bookatz and Shamseddine2, Reference Shamseddine12]. In the following section, we will generalize in Definition 5 and Definition 6 the concepts of WLUD$^{k}$![]() and WLUD$^{\infty }$
and WLUD$^{\infty }$![]() to functions from $\mathcal {N}^{n}$
to functions from $\mathcal {N}^{n}$![]() to $\mathcal {N}$
to $\mathcal {N}$![]() ; and we will formulate (in Theorem 8 and Theorem 9 and their proofs) conditions under which a WLUD$^{\infty }$
; and we will formulate (in Theorem 8 and Theorem 9 and their proofs) conditions under which a WLUD$^{\infty }$![]() $\mathcal {N}$
$\mathcal {N}$![]() -valued function at a point $x_0\in \mathcal {N}$
-valued function at a point $x_0\in \mathcal {N}$![]() or a WLUD$^{\infty }$
or a WLUD$^{\infty }$![]() $\mathcal {N}$
$\mathcal {N}$![]() -valued function at a point $\boldsymbol {x_0} \in \mathcal {N}^{n}$
-valued function at a point $\boldsymbol {x_0} \in \mathcal {N}^{n}$![]() will be analytic at that point.
will be analytic at that point.
Theorem 8 Let $A \subseteq \mathcal {N}$![]() be open, let $x_0\in A,$
be open, let $x_0\in A,$![]() and let $f : A \rightarrow \mathcal {N}$
and let $f : A \rightarrow \mathcal {N}$![]() be WLUD$^{\infty }$
be WLUD$^{\infty }$![]() at $x_0$
at $x_0$![]() . For each $k\in \mathbb {N},$
. For each $k\in \mathbb {N},$![]() let $\delta _k>0$
let $\delta _k>0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() correspond to $\epsilon =1$
correspond to $\epsilon =1$![]() in Definition 2. Assume that
in Definition 2. Assume that

Then, there exists a neighbourhood $U$![]() of $x_0$
of $x_0$![]() in $A$
in $A$![]() such that, for any $x,\,y \in U$
such that, for any $x,\,y \in U$![]() , we have that
, we have that

That is, the Taylor series $\sum \nolimits \limits _{j=0}^{\infty } \frac {f^{(j)}(x)}{j!}(y-x)^{j}$![]() converges in $\mathcal {N}$
converges in $\mathcal {N}$![]() to $f(y);$
to $f(y);$![]() and hence $f$
and hence $f$![]() is analytic in $U$
is analytic in $U$![]() .
.
Proof. First, we note that

Thus, the Taylor series $\sum \nolimits \limits _{j=0}^{\infty } \frac {f^{(j)}(x_0)}{j!}(x-x_0)^{j}$![]() of $f$
of $f$![]() at $x_0$
at $x_0$![]() has a positive radius of convergence [Reference Schikhof9]
has a positive radius of convergence [Reference Schikhof9]

Let

Then, $\lambda _0\in \mathbb {R}$![]() and $\lambda _0<\infty$
and $\lambda _0<\infty$![]() . Then, for all $x\in \mathcal {N}$
. Then, for all $x\in \mathcal {N}$![]() satisfying $\lambda (x-x_0)>\lambda _0$
satisfying $\lambda (x-x_0)>\lambda _0$![]() , we have that
, we have that

Thus, for all $x\in \mathcal {N}$![]() satisfying $\lambda (x-x_0)>\lambda _0$
satisfying $\lambda (x-x_0)>\lambda _0$![]() , we have that $|x-x_0|_v< R$
, we have that $|x-x_0|_v< R$![]() and, by [Reference Schikhof9, p. 59], $\sum \nolimits \limits _{j=0}^{\infty } \frac {f^{(j)}(x_0)}{j!}(x-x_0)^{j}$
and, by [Reference Schikhof9, p. 59], $\sum \nolimits \limits _{j=0}^{\infty } \frac {f^{(j)}(x_0)}{j!}(x-x_0)^{j}$![]() converges in $(\mathcal {N},\,\tau _v)$
converges in $(\mathcal {N},\,\tau _v)$![]() ; that is, it converges with respect to both the ultrametric absolute value $|\cdot |_v$
; that is, it converges with respect to both the ultrametric absolute value $|\cdot |_v$![]() and the ordinary absolute value $|\cdot |$
and the ordinary absolute value $|\cdot |$![]() .
.
For all $k\in \mathbb {N}$![]() , we have that $(x_0-\delta _k,\, x_0+\delta _k)\subset A$
, we have that $(x_0-\delta _k,\, x_0+\delta _k)\subset A$![]() , $f$
, $f$![]() is $k$
is $k$![]() times differentiable on $(x_0-\delta _k,\, x_0+\delta _k)$
times differentiable on $(x_0-\delta _k,\, x_0+\delta _k)$![]() , and
, and

Since $\limsup \limits _{k\rightarrow \infty }\lambda (\delta _k)<\infty$![]() , there exists $t>0$
, there exists $t>0$![]() in $\mathbb {Q}$
in $\mathbb {Q}$![]() such that $\limsup \limits _{k\rightarrow \infty }\lambda (\delta _k)< t<\infty$
such that $\limsup \limits _{k\rightarrow \infty }\lambda (\delta _k)< t<\infty$![]() . Thus, there exists $N\in \mathbb {N}$
. Thus, there exists $N\in \mathbb {N}$![]() such that
such that
Let $\delta >0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() be such that $\lambda (\delta )>\max \{\lambda _0,\, t,\,0\}$
be such that $\lambda (\delta )>\max \{\lambda _0,\, t,\,0\}$![]() ; this is possible since $\max \{\lambda _0,\, t,\,0\}<\infty$
; this is possible since $\max \{\lambda _0,\, t,\,0\}<\infty$![]() . It follows from (2) that $\lambda (\delta )>\lambda (\delta _k)$
. It follows from (2) that $\lambda (\delta )>\lambda (\delta _k)$![]() and hence $0<\delta \ll \delta _k$
and hence $0<\delta \ll \delta _k$![]() for all $k>N$
for all $k>N$![]() . Thus, $(x_0-\delta,\, x_0+\delta )\subset A$
. Thus, $(x_0-\delta,\, x_0+\delta )\subset A$![]() , $f$
, $f$![]() is infinitely often differentiable on $(x_0-\delta,\, x_0+\delta )$
is infinitely often differentiable on $(x_0-\delta,\, x_0+\delta )$![]() , and
, and
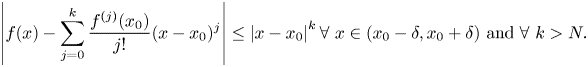
Moreover, for all $x\in (x_0-\delta,\, x_0+\delta )$![]() , we have that $\lambda (x-x_0)\ge \lambda (\delta )>\lambda _0$
, we have that $\lambda (x-x_0)\ge \lambda (\delta )>\lambda _0$![]() and hence $\sum \nolimits \limits _{j=0}^{\infty } \frac {f^{(j)}(x_0)}{j!}(x-x_0)^{j}$
and hence $\sum \nolimits \limits _{j=0}^{\infty } \frac {f^{(j)}(x_0)}{j!}(x-x_0)^{j}$![]() converges in $\mathcal {N}$
converges in $\mathcal {N}$![]() . Let $U=(x_0-\delta,\, x_0+\delta )$
. Let $U=(x_0-\delta,\, x_0+\delta )$![]() .
.
First, we show that

Let $x\in U$![]() be given. Taking the limit in (3) as $k\rightarrow \infty$
be given. Taking the limit in (3) as $k\rightarrow \infty$![]() , we get:
, we get:

from which we obtain

Since $\lambda (x-x_0)\ge \lambda (\delta )>0$![]() , we obtain that $\lim \limits _{k\rightarrow \infty } \left |x-x_0\right |^{k}=0$
, we obtain that $\lim \limits _{k\rightarrow \infty } \left |x-x_0\right |^{k}=0$![]() . It follows that
. It follows that

from which we infer that $f(x)=\sum \nolimits \limits _{j=0}^{\infty } \frac {f^{(j)}(x_0)}{j!}(x-x_0)^{j}$![]() or, equivalently,
or, equivalently,
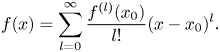
Since the convergence of the Taylor series above is in the order (valuation) topology, we will show that the derivatives of $f$![]() at $x$
at $x$![]() to any order are obtained by differentiating the power series in Equation (4) term by term. That is, for all $j\in \mathbb {N}$
to any order are obtained by differentiating the power series in Equation (4) term by term. That is, for all $j\in \mathbb {N}$![]() ,
,
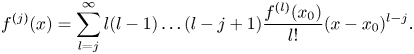
First, note that since $\lambda (l(l-1)\ldots (l-j+1))=0$![]() , it follows that $\sum \nolimits _{l=j}^{\infty } l(l-1)\ldots (l-j+1)\frac {f^{(l)}(x_0)}{l!}(x-x_0)^{l-j}$
, it follows that $\sum \nolimits _{l=j}^{\infty } l(l-1)\ldots (l-j+1)\frac {f^{(l)}(x_0)}{l!}(x-x_0)^{l-j}$![]() converges in $\mathcal {N}$
converges in $\mathcal {N}$![]() for all $j\in \mathbb {N}$
for all $j\in \mathbb {N}$![]() . Using induction on $j$
. Using induction on $j$![]() , it suffices to show that
, it suffices to show that

Let $h\in \mathcal {N}$![]() be such that $x+h\in U$
be such that $x+h\in U$![]() . We will show that
. We will show that

Thus,

Now, let $y\in U$![]() be given. Then
be given. Then

Since convergence in the order topology (valuation topology) entails absolute convergence, we can interchange the order of the summations in the last equality [Reference Shamseddine10, Reference Shamseddine and Berz14]. We get:

where we made use of Equation (5) in the last step.
Replacing $m$![]() by $1$
by $1$![]() in Definition 3, then the $m\times n$
in Definition 3, then the $m\times n$![]() matrix $\boldsymbol {D}\boldsymbol {f}(\boldsymbol {x})$
matrix $\boldsymbol {D}\boldsymbol {f}(\boldsymbol {x})$![]() is replaced by the gradient of $\boldsymbol {f}$
is replaced by the gradient of $\boldsymbol {f}$![]() at $\boldsymbol {x}$
at $\boldsymbol {x}$![]() : $\boldsymbol {\nabla }f(\boldsymbol {x})$
: $\boldsymbol {\nabla }f(\boldsymbol {x})$![]() , and we readily obtain the definition of a WLUD $\mathcal {N}$
, and we readily obtain the definition of a WLUD $\mathcal {N}$![]() -valued function at a point $\boldsymbol {x_0}$
-valued function at a point $\boldsymbol {x_0}$![]() or on an open subset $A$
or on an open subset $A$![]() of $\mathcal {N}^{n}$
of $\mathcal {N}^{n}$![]() .
.
Definition 4 Let $A\subset \mathcal {N}^{n}$![]() be open, let $f:A \to \mathcal {N}$
be open, let $f:A \to \mathcal {N}$![]() , and let $\boldsymbol {x_0}\in A$
, and let $\boldsymbol {x_0}\in A$![]() be given. Then, we say that $f$
be given. Then, we say that $f$![]() is WLUD at $\boldsymbol {x_0}$
is WLUD at $\boldsymbol {x_0}$![]() if $f$
if $f$![]() is differentiable in a neighbourhood $\Omega$
is differentiable in a neighbourhood $\Omega$![]() of $\boldsymbol {x_0}$
of $\boldsymbol {x_0}$![]() in $A$
in $A$![]() and if for every $\epsilon >0$
and if for every $\epsilon >0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() there exists $\delta >0$
there exists $\delta >0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() such that $B_{\delta }(\boldsymbol {x_0})\subset \Omega$
such that $B_{\delta }(\boldsymbol {x_0})\subset \Omega$![]() , and for all $\boldsymbol {x},\,\boldsymbol {y}\in B_{\delta }(\boldsymbol {x_0})$
, and for all $\boldsymbol {x},\,\boldsymbol {y}\in B_{\delta }(\boldsymbol {x_0})$![]() we have that
we have that
Moreover, we say that $f$![]() is WLUD on $A$
is WLUD on $A$![]() if $f$
if $f$![]() is WLUD at every point in $A$
is WLUD at every point in $A$![]() .
.
Using Definition 2 and Definition 4, the natural way to define $k$![]() times weak local uniform differentiability (WLUD$^{k}$
times weak local uniform differentiability (WLUD$^{k}$![]() ) at a point $\boldsymbol {x_0}$
) at a point $\boldsymbol {x_0}$![]() or on an open subset $A$
or on an open subset $A$![]() of $\mathcal {N}^{n}$
of $\mathcal {N}^{n}$![]() is as follows.
is as follows.
Definition 5 Let $A\subset \mathcal {N}^{n}$![]() be open, let $f:A \to \mathcal {N}$
be open, let $f:A \to \mathcal {N}$![]() , and let $\boldsymbol {x_0}\in A$
, and let $\boldsymbol {x_0}\in A$![]() be given. Then, we say that $f$
be given. Then, we say that $f$![]() is WLUD$^{k}$
is WLUD$^{k}$![]() at $\boldsymbol {x_0}$
at $\boldsymbol {x_0}$![]() if $f$
if $f$![]() is $k$
is $k$![]() -times differentiable in a neighbourhood $\Omega$
-times differentiable in a neighbourhood $\Omega$![]() of $\boldsymbol {x_0}$
of $\boldsymbol {x_0}$![]() in $A$
in $A$![]() and if for every $\epsilon >0$
and if for every $\epsilon >0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() there exists $\delta >0$
there exists $\delta >0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() such that $B_{\delta }(\boldsymbol {x_0})\subset \Omega$
such that $B_{\delta }(\boldsymbol {x_0})\subset \Omega$![]() , and for all $\boldsymbol {\xi },\,\boldsymbol {\eta }\in B_{\delta }(\boldsymbol {x_0})$
, and for all $\boldsymbol {\xi },\,\boldsymbol {\eta }\in B_{\delta }(\boldsymbol {x_0})$![]() we have that
we have that

where

Moreover, we say that $f$![]() is WLUD$^{k}$
is WLUD$^{k}$![]() on $A$
on $A$![]() if $f$
if $f$![]() is WLUD$^{k}$
is WLUD$^{k}$![]() at every point in $A$
at every point in $A$![]() .
.
Definition 6 Let $A\subset \mathcal {N}^{n}$![]() be open, let $f:A \to \mathcal {N}$
be open, let $f:A \to \mathcal {N}$![]() , and let $\boldsymbol {x_0}\in A$
, and let $\boldsymbol {x_0}\in A$![]() be given. Then, we say that $f$
be given. Then, we say that $f$![]() is WLUD$^{\infty }$
is WLUD$^{\infty }$![]() at $\boldsymbol {x_0}$
at $\boldsymbol {x_0}$![]() if $f$
if $f$![]() is WLUD$^{k}$
is WLUD$^{k}$![]() at $\boldsymbol {x_0}$
at $\boldsymbol {x_0}$![]() for every $k\in \mathbb {N}$
for every $k\in \mathbb {N}$![]() . Moreover, we say that $f$
. Moreover, we say that $f$![]() is WLUD$^{\infty }$
is WLUD$^{\infty }$![]() on $A$
on $A$![]() if $f$
if $f$![]() is WLUD$^{\infty }$
is WLUD$^{\infty }$![]() at every point in $A$
at every point in $A$![]() .
.
Now, we are ready to state and prove the analogue of Theorem 8 for functions of $n$![]() variables.
variables.
Theorem 9 Let $A \subseteq \mathcal {N}^{n}$![]() be open, let $\boldsymbol {x_0}\in A,$
be open, let $\boldsymbol {x_0}\in A,$![]() and let $f : A \rightarrow \mathcal {N}$
and let $f : A \rightarrow \mathcal {N}$![]() be WLUD$^{\infty }$
be WLUD$^{\infty }$![]() at $\boldsymbol {x_0}$
at $\boldsymbol {x_0}$![]() . For each $k\in \mathbb {N},$
. For each $k\in \mathbb {N},$![]() let $\delta _k>0$
let $\delta _k>0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() correspond to $\epsilon =1$
correspond to $\epsilon =1$![]() in Definition 5. Assume that
in Definition 5. Assume that

Then, there exists a neighbourhood $U$![]() of $\boldsymbol {x_0}$
of $\boldsymbol {x_0}$![]() in $A$
in $A$![]() such that, for any $\boldsymbol {\eta }\in U,$
such that, for any $\boldsymbol {\eta }\in U,$![]() we have that
we have that

Proof. Let

Then, $\lambda _0\in \mathbb {R}$![]() and $\lambda _0<\infty$
and $\lambda _0<\infty$![]() .
.
For all $k\in \mathbb {N}$![]() , we have that $B_{\delta _k}(\boldsymbol {x_0})\subset A$
, we have that $B_{\delta _k}(\boldsymbol {x_0})\subset A$![]() , $f$
, $f$![]() is $k$
is $k$![]() times differentiable on $B_{\delta _k}(\boldsymbol {x_0})$
times differentiable on $B_{\delta _k}(\boldsymbol {x_0})$![]() , and
, and

Since $\limsup \limits _{k\rightarrow \infty }\lambda (\delta _k)<\infty$![]() , there exists $t>0$
, there exists $t>0$![]() in $\mathbb {Q}$
in $\mathbb {Q}$![]() such that $\limsup \limits _{k\rightarrow \infty }\lambda (\delta _k)< t<\infty$
such that $\limsup \limits _{k\rightarrow \infty }\lambda (\delta _k)< t<\infty$![]() . Thus, there exists $N\in \mathbb {N}$
. Thus, there exists $N\in \mathbb {N}$![]() such that
such that
Let $\delta >0$![]() in $\mathcal {N}$
in $\mathcal {N}$![]() be such that $\lambda (\delta )>\max \{\lambda _0,\, t,\,0\}$
be such that $\lambda (\delta )>\max \{\lambda _0,\, t,\,0\}$![]() . It follows from (6) that $\lambda (\delta )>\lambda (\delta _k)$
. It follows from (6) that $\lambda (\delta )>\lambda (\delta _k)$![]() and hence $0<\delta \ll \delta _k$
and hence $0<\delta \ll \delta _k$![]() for all $k>N$
for all $k>N$![]() . Thus, $B_{\delta }(\boldsymbol {x_0})\subset A$
. Thus, $B_{\delta }(\boldsymbol {x_0})\subset A$![]() , $f$
, $f$![]() is infinitely often differentiable on $B_{\delta }(\boldsymbol {x_0})$
is infinitely often differentiable on $B_{\delta }(\boldsymbol {x_0})$![]() , and
, and

Let $U=B_{\delta }(\boldsymbol {x_0})$![]() ; and let $\boldsymbol {\eta }\in U$
; and let $\boldsymbol {\eta }\in U$![]() be given. Then, we have that $\lambda (\vert \boldsymbol {\eta } - \boldsymbol {x_0} \vert )\ge \lambda (\delta )>\lambda _0$
be given. Then, we have that $\lambda (\vert \boldsymbol {\eta } - \boldsymbol {x_0} \vert )\ge \lambda (\delta )>\lambda _0$![]() . We will show first that $\sum \nolimits _{j=1}^{\infty } \frac {1}{j!}[(\boldsymbol {\eta }-\boldsymbol {x_0})\cdot \nabla ]^{j}f(\boldsymbol {x_0})$
. We will show first that $\sum \nolimits _{j=1}^{\infty } \frac {1}{j!}[(\boldsymbol {\eta }-\boldsymbol {x_0})\cdot \nabla ]^{j}f(\boldsymbol {x_0})$![]() converges in $\mathcal {N}$
converges in $\mathcal {N}$![]() . Since $\lambda (\vert \boldsymbol {\eta } - \boldsymbol {x_0} \vert )>\lambda _0$
. Since $\lambda (\vert \boldsymbol {\eta } - \boldsymbol {x_0} \vert )>\lambda _0$![]() , there exists $q>0$
, there exists $q>0$![]() in $\mathbb {Q}$
in $\mathbb {Q}$![]() such that $\lambda (\vert \boldsymbol {\eta } - \boldsymbol {x_0} \vert )-q>\lambda _0$
such that $\lambda (\vert \boldsymbol {\eta } - \boldsymbol {x_0} \vert )-q>\lambda _0$![]() . Hence, there exists $M\in \mathbb {N}$
. Hence, there exists $M\in \mathbb {N}$![]() such that
such that

for all $j>M$![]() and for $l_1=1,\, \ldots,\, n$
and for $l_1=1,\, \ldots,\, n$![]() , $l_2=1,\, \ldots,\, n$
, $l_2=1,\, \ldots,\, n$![]() , …, $l_j=1,\, \ldots,\, n$
, …, $l_j=1,\, \ldots,\, n$![]() . It follows that
. It follows that

for all $j>M$![]() and for $l_1=1,\, \ldots,\, n$
and for $l_1=1,\, \ldots,\, n$![]() , $l_2=1,\, \ldots,\, n$
, $l_2=1,\, \ldots,\, n$![]() , …, $l_j=1,\, \ldots,\, n$
, …, $l_j=1,\, \ldots,\, n$![]() . Thus,
. Thus,

for all $j>M$![]() ; and hence
; and hence
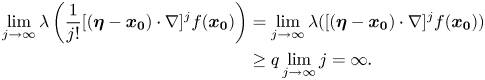
Thus,
and hence $\sum \nolimits _{j=1}^{\infty } \frac {1}{j!}[(\boldsymbol {\eta }-\boldsymbol {x_0})\cdot \nabla ]^{j}f(\boldsymbol {x_0})$![]() converges in $\mathcal {N}$
converges in $\mathcal {N}$![]() ; that is,
; that is,

Taking the limit in (7) as $k\rightarrow \infty$![]() , we get:
, we get:
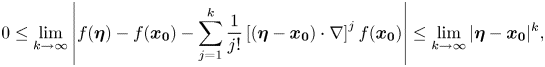
from which we obtain

Since $\lambda (\vert \boldsymbol {\eta } - \boldsymbol {x_0}\vert )\ge \lambda (\delta )>0$![]() , we obtain that $\lim \limits _{k\rightarrow \infty } \left |\boldsymbol {\eta } - \boldsymbol {x_0}\right |^{k}=0$
, we obtain that $\lim \limits _{k\rightarrow \infty } \left |\boldsymbol {\eta } - \boldsymbol {x_0}\right |^{k}=0$![]() . It follows that
. It follows that

from which we infer that

Acknowledgements
This research was funded by the Natural Sciences and Engineering Council of Canada (NSERC, Grant # RGPIN/4965-2017)
Competing interests declaration
The author has no conflicts of interest to declare.