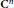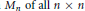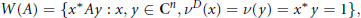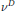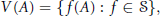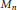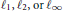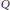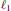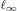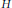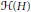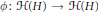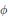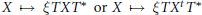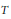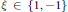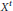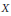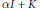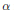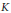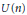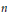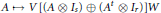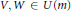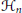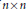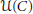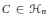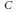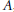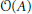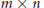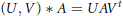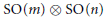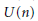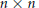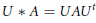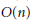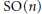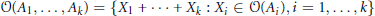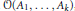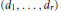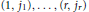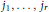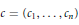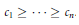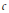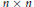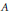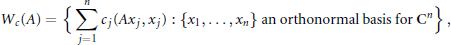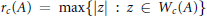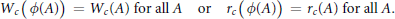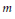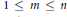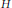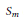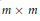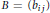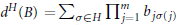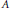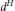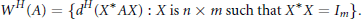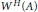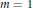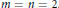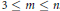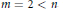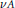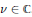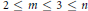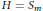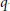24 results
Factoring a Quadratic Operator as a Product of Two Positive Contractions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 354-362
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
Sum of Hermitian Matrices with Given Eigenvalues: Inertia, Rank, and Multiple Eigenvalues
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 109-132
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
SPECTRUM, NUMERICAL RANGE AND DAVIS-WIELANDT SHELL OF A NORMAL OPERATOR
-
- Journal:
- Glasgow Mathematical Journal / Volume 51 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 91-100
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
SCHUR MULTIPLICATIVE MAPS ON MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 49-72
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Numerical Range of the Derivation of an Induced Operator
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 325-344
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Mappings on matrices: invariance of functional values of matrix products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-184
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Schottky Source/Drain Transistor on Thin SiGe on Insulator Integrated with HfO2/TaN Gate Stack
-
- Journal:
- MRS Online Proceedings Library Archive / Volume 913 / 2006
- Published online by Cambridge University Press:
- 01 February 2011, 0913-D01-04
- Print publication:
- 2006
-
- Article
- Export citation
Isometries between matrix algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-16
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
Linear Operators on Matrix Algebras that Preserve the Numerical Range, Numerical Radius or the States
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 1 / 01 February 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 134-167
- Print publication:
- 01 February 2004
-
- Article
-
- You have access
- Export citation
Linear maps leaving invariant subsets of nonnegative symmetric matrices
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 68 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 17 April 2009, pp. 221-231
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
Linear Maps on Selfadjoint Operators Preserving Invertibility, Positive Definiteness, Numerical Range
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 2 / 01 June 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 216-228
- Print publication:
- 01 June 2003
-
- Article
-
- You have access
- Export citation
Linear Maps Transforming the Unitary Group
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 1 / 01 March 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 54-58
- Print publication:
- 01 March 2003
-
- Article
-
- You have access
- Export citation
Some Convexity Features Associated with Unitary Orbits
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 1 / 01 February 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 91-111
- Print publication:
- 01 February 2003
-
- Article
-
- You have access
- Export citation
H-joint numerical ranges
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 66 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 17 April 2009, pp. 105-117
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
Diagonals and Partial Diagonals of Sum of Matrices
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 3 / 01 June 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 571-594
- Print publication:
- 01 June 2002
-
- Article
-
- You have access
- Export citation
Linear Operators Preserving Generalized Numerical Ranges and Radii on Certain Triangular Algebras of Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 3 / 01 September 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 270-281
- Print publication:
- 01 September 2001
-
- Article
-
- You have access
- Export citation
Nonconvexity of the Generalized Numerical Range Associated with the Principal Character
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 4 / 01 December 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 448-458
- Print publication:
- 01 December 2000
-
- Article
-
- You have access
- Export citation
Numerical Ranges Arising from Simple Lie Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 1 / 01 February 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 141-171
- Print publication:
- 01 February 2000
-
- Article
-
- You have access
- Export citation
Extension of stochastic dominance theory to random variables
-
- Journal:
- RAIRO - Operations Research / Volume 33 / Issue 4 / October 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 509-524
- Print publication:
- October 1999
-
- Article
- Export citation
Perfect codes on the towers of Hanoi graph
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 57 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 17 April 2009, pp. 367-376
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation



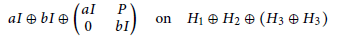
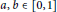

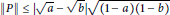
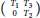
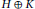
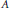

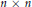
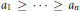
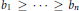
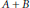

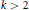
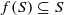 for different subsets
for different subsets 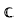 , let
, let 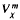 (
(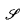 of complex numbers such that
of complex numbers such that