Hostname: page-component-84b7d79bbc-g5fl4 Total loading time: 0 Render date: 2024-07-30T07:41:55.573Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical Ranges Arising from Simple Lie Algebras

Published online by Cambridge University Press:  20 November 2018

Chi-Kwong Li  and
Tin-Yau Tam
Chi-Kwong Li
Affiliation:
Department of Mathematics, College of William and Mary, P.O. Box 8795, Williamburg, VA 23187-8795, USA email: chkli@math.wm.edu website: http://www.math.wm.edu/~ckli
Tin-Yau Tam
Affiliation:
Department of Mathematics, Auburn University, Auburn, AL 36849-5310, USA email: tamtiny@mail.auburn.edu website: http://www.auburn.edu/~tamtiny
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A unified formulation is given to various generalizations of the classical numerical range including the $c$-numerical range, congruence numerical range, 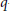$q$-numerical range and von Neumann range. Attention is given to those cases having connections with classical simple real Lie algebras. Convexity and inclusion relation involving those generalized numerical ranges are investigated. The underlying geometry is emphasized.

Keywords

15A6017B20numerical rangeconvexityinclusion relation
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 1 , 01 February 2000 , pp. 141 - 171
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Au-Yeung, Y. H. and Poon, Y. T., A remark on the convexity and positive definiteness concerning Hermitian matrices. Southeast Asian Bull. Math. 3 (1979), 85–92.Google Scholar
[2] Au-Yeung, Y. H. and Tsing, N. K., An extension of the Hausdorff-Toeplitz theorem. Proc. Amer. Math. Soc. 89 (1983), 215–218.Google Scholar
[3] Au-Yeung, Y. H. and Tsing, N. K., Some theorems on the numerical range. Linear and Multilinear Algebra 15 (1984), 215–218.Google Scholar
[4] Berger, C. A., Normal Dilations. Ph.D. dissertation, Cornell University, 1963.Google Scholar
[5] Brickman, L., On the field of values of a matrix. Proc. Amer. Math. Soc. 12 (1961), 61–66.Google Scholar
[6] Choi, M. D., Laurie, C., Radjavi, H. and Rosenthal, P., On the congruence numerical range and related functions of matrices. Linear and Multilinear Algebra 22 (1987), 1–5.Google Scholar
[7] Chong, K. M., An induction theorem for rearrangements. Canad. J. Math. 28 (1976), 154–160.Google Scholar
[8] Davis, C., The Toeplitz-Haudorff theorem explained. Canad. Math. Bull. 14 (1971), 245–246.Google Scholar
[9] Goldberg, M. and Straus, E. G., Elementary inclusion relations for generalized numerical ranges. Linear Algebra Appl. 18 (1977), 1–24.Google Scholar
[10] Gustafson, K. E. and Rao, D. K. M., Numerical Range: the field of values of linear operators and matrices. Springer, New York, 1997.Google Scholar
[11] Halmos, P., A Hilbert Space Problem Book. Springer-Verlag, New York, 1982.Google Scholar
[12] Hausdorff, F., Der Wertvorrat einer Bilinearform. Math Z. 3 (1919), 314–316.Google Scholar
[13] Helgason, S., Differential Geometry, Lie Groups and Symmetric Spaces. Academic Press, New York, 1978.Google Scholar
[14] Horn, R. A. and Johnson, C. R., Topics in Matrix Analysis. Cambridge University Press, Cambridge, 1991.Google Scholar
[15] Knapp, A. W., Representation Theory of Semisimple Groups. Princeton University Press, New Jersey, 1986.Google Scholar
[16] Kostant, B., On convexity, the Weyl group and Iwasawa decomposition. Ann. Sci. Ecole Norm. Sup. (4) 6 (1973), 413–460.Google Scholar
[17] Li, C. K., Matrices with some extremal properties. Linear Algebra Appl. 101 (1988), 255–267.Google Scholar
[18] Li, C. K., C-numerical ranges and C-numerical radii. Linear and Multilinear Algebra 37 (1994), 51–82.Google Scholar
[19] Li, C. K., Some convexity theorems for the generalized numerical ranges. Linear and Multilinear Algebra 40 (1996), 235–240.Google Scholar
[20] Li, C. K. and Nakazato, H., Some results on the q-numerical range. Linear and Multilinear Algebra 43 (1998), 385–410.Google Scholar
[21] Miranda, H. and Thompson, R. C., A supplement to the von Neumann trace inequality for singular values. Linear Algebra Appl. 248 (1994), 61–66.Google Scholar
[22] von Neumann, J., Some matrix-inequalities and metrization of matrix-space. Tomsk. Univ. Rev. 1 (1937), 286–300. In: Collected Works, Pergamon, New York, 1962, Vol. 4, 205–219.Google Scholar
[23] Onishchik, A. L. and Vinberg, E. B., Lie groups and algebraic groups. Springer-Verlag, Berlin, 1990.Google Scholar
[24] Poon, Y. T., Another proof of a result of Westwick. Linear and Multilinear Algebra 9 (1980), 35–37.Google Scholar
[25] Poon, Y. T., Generalized numerical ranges, joint positive definiteness and multiple eigenvalues. Proc. Amer. Math. Soc. 125 (1997), 1625–1634.Google Scholar
[26] Tam, T. Y., Note on a paper of Thompson: the congruence numerical range. Linear and Multilinear Algebra 17 (1985), 107–115.Google Scholar
[27] Tam, T. Y., Kostant's convexity theorem and the compact classical groups. Linear and Multilinear Algebra 43 (1997), 87–113.Google Scholar
[28] Tam, T. Y.,Miranda and Thompson's trace inequality and a log convexity result. Linear Algebra Appl. 262 (1997), 307–325.Google Scholar
[29] Tam, T. Y., Partial superdiagonal elements and singular values of a complex skew symmetric matrix. SIAM J. Matrix Anal. Appl. 19 (1998), 737–754.Google Scholar
[30] Tam, T. Y., An extension of a convexity theorem of the generalized numerical range associated with SO(2n + 1). Proc. Amer. Math. Soc. (1) 127 (1999), 35–44.Google Scholar
[31] Tam, T. Y., Generalized numerical ranges, numerical radii, and Lie groups. Manuscript, 1996.Google Scholar
[32] Tam, T. Y., A Lie theoretic approach of Thompson's theorems on singular values-diagonal elements and some related results. J. London Math. Soc., to appear.Google Scholar
[33] Tam, T. Y., Group majorization, Eaton triples and numerical range. Linear and Multilinear Algebra, to appear.Google Scholar
[34] Tamand, T. Y., Tsing, N. K., Research problem: the congruence numerical range. Linear and Multilinear Algebra 19 (1986), 405.Google Scholar
[35] Thompson, R. C., Singular values, diagonal elements and convexity. SIAM J. Appl. Math. 32 (1977), 39–63.Google Scholar
[36] Thompson, R. C., Singular values and diagonal elements of complex symmetric matrices. Linear Algebra Appl. 26 (1979), 65–106.Google Scholar
[37] Thompson, R. C., The congruence numerical range. Linear and Multilinear Algebra 8 (1980), 197–206.Google Scholar
[38] Toeplitz, O., Das algebraische Analogon zu einem Satze von Fejér. Math. Z. 2 (1918), 187–197.Google Scholar
[39] Tsing, N. K., The constrainted bilinear form and the C-numerical range. Linear Algebra Appl. 56 (1984), 195–206.Google Scholar
[40] Warmer, F., Foundation of Differentiable manifolds and Lie Groups. Scott Foresman and Company, 1971.Google Scholar
[41] Westwick, R., A theorem on numerical range. Linear and Multilinear Algebra 2 (1975), 311–315.Google Scholar