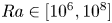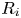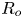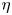83 results
Childhood socio-economic disadvantages versus adverse care experiences: Mediation and moderation impacts on late-life depressive symptoms
-
- Journal:
- European Psychiatry / Volume 67 / Issue 1 / 2024
- Published online by Cambridge University Press:
- 27 August 2024, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bone-artefact production in late Neolithic central China: evidence from Pingliangtai
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Photo-assisted Catalytic Removal of NOx Over La1–xPrxCoO3/Palygorskite Nanocomposites: Role of Pr Doping
-
- Journal:
- Clays and Clay Minerals / Volume 67 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 01 January 2024, pp. 348-356
-
- Article
- Export citation
Tuning the Acidity of Montmorillonite by H3PO4-Activation and Supporting WO3 for Catalytic Dehydration of Glycerol to Acrolein
-
- Journal:
- Clays and Clay Minerals / Volume 70 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 01 January 2024, pp. 460-479
-
- Article
- Export citation
Brain functional changes across mood states in bipolar disorder: from a large-scale network perspective
-
- Journal:
- Psychological Medicine / Volume 54 / Issue 4 / March 2024
- Published online by Cambridge University Press:
- 12 December 2023, pp. 763-774
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moral emotions underlie puritanical morality
-
- Journal:
- Behavioral and Brain Sciences / Volume 46 / 2023
- Published online by Cambridge University Press:
- 04 October 2023, e321
-
- Article
- Export citation
X-ray diffraction performance of thermally distorted crystals
-
- Journal:
- High Power Laser Science and Engineering / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 July 2023, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intermittent fasting promotes adipocyte mitochondrial fusion through Sirt3-mediated deacetylation of Mdh2
-
- Journal:
- British Journal of Nutrition / Volume 130 / Issue 9 / 14 November 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 1473-1486
- Print publication:
- 14 November 2023
-
- Article
-
- You have access
- HTML
- Export citation
Power Transmission Network Optimization Strategy Based on Random Fractal Beetle Antenna Algorithm
-
- Journal:
- Wireless Power Transfer / Volume 2023 / 2023
- Published online by Cambridge University Press:
- 01 January 2024, e1
- Print publication:
- 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effects of radius ratio on annular centrifugal Rayleigh–Bénard convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 930 / 10 January 2022
- Published online by Cambridge University Press:
- 10 November 2021, A19
-
- Article
- Export citation
Expanding the capabilities of the RF stroboscopic TEM
-
- Journal:
- Microscopy and Microanalysis / Volume 27 / Issue S1 / August 2021
- Published online by Cambridge University Press:
- 30 July 2021, p. 2708
- Print publication:
- August 2021
-
- Article
-
- You have access
- Export citation
Contents
-
- Book:
- Dynamics of Multiphase Flows
- Published online:
- 10 September 2021
- Print publication:
- 17 June 2021, pp ix-xviii
-
- Chapter
- Export citation
10 - Fluidization
- from Part II - Application-Based Analysis of Multiphase Flows
-
- Book:
- Dynamics of Multiphase Flows
- Published online:
- 10 September 2021
- Print publication:
- 17 June 2021, pp 423-476
-
- Chapter
- Export citation
11 - Pipe Flow
- from Part II - Application-Based Analysis of Multiphase Flows
-
- Book:
- Dynamics of Multiphase Flows
- Published online:
- 10 September 2021
- Print publication:
- 17 June 2021, pp 477-525
-
- Chapter
- Export citation
9 - Separation of Multiphase Flows
- from Part II - Application-Based Analysis of Multiphase Flows
-
- Book:
- Dynamics of Multiphase Flows
- Published online:
- 10 September 2021
- Print publication:
- 17 June 2021, pp 377-422
-
- Chapter
- Export citation
7 - Numerical Modeling and Simulation
- from Part I - Principles
-
- Book:
- Dynamics of Multiphase Flows
- Published online:
- 10 September 2021
- Print publication:
- 17 June 2021, pp 261-315
-
- Chapter
- Export citation
1 - Introduction to Multiphase Flows
- from Part I - Principles
-
- Book:
- Dynamics of Multiphase Flows
- Published online:
- 10 September 2021
- Print publication:
- 17 June 2021, pp 3-30
-
- Chapter
- Export citation
Dedication
-
- Book:
- Dynamics of Multiphase Flows
- Published online:
- 10 September 2021
- Print publication:
- 17 June 2021, pp vii-viii
-
- Chapter
- Export citation
Part II - Application-Based Analysis of Multiphase Flows
-
- Book:
- Dynamics of Multiphase Flows
- Published online:
- 10 September 2021
- Print publication:
- 17 June 2021, pp 375-376
-
- Chapter
- Export citation