44 results
Finite skew braces of square-free order and supersolubility
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 March 2024, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISED MUTUALLY PERMUTABLE PRODUCTS AND SATURATED FORMATIONS, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 30 January 2024, pp. 1-11
-
- Article
- Export citation
FINITE GROUPS WITH HEREDITARILY G-PERMUTABLE SCHMIDT SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Jordan–Hölder theorem for skew left braces and their applications to multipermutation solutions of the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some products of finite groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 28 March 2023, pp. 89-99
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME PRODUCTS OF SUBGROUPS AND VANISHING CONJUGACY CLASS SIZES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 271-275
- Print publication:
- April 2023
-
- Article
- Export citation
ON CERTAIN PRODUCTS OF PERMUTABLE SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 16 August 2021, pp. 278-285
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Left Braces and the Quantum Yang–Baxter Equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 595-608
-
- Article
- Export citation
A NOTE ON NORMAL COMPLEMENTS FOR FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 109-112
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
ON A THEOREM OF KANG AND LIU ON FACTORISED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 08 November 2017, pp. 54-56
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
SEMIPERMUTABILITY IN GENERALISED SOLUBLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 219-227
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
Triple Factorizations and Supersolubility of Finite Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 11 June 2015, pp. 301-309
-
- Article
- Export citation
ON GENERALISED PRONORMAL SUBGROUPS OF FINITE GROUPS
-
- Journal:
- Glasgow Mathematical Journal / Volume 56 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 August 2014, pp. 691-703
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
ON A CLASS OF SUPERSOLUBLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 23 May 2014, pp. 220-226
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
PRIMITIVE SUBGROUPS AND PST-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 373-378
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
ON CONJUGACY OF SUPPLEMENTS OF NORMAL SUBGROUPS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 293-299
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
SOME SOLUBILITY CRITERIA IN FACTORISED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 22-28
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
SUBGROUPS OF FINITE GROUPS WITH A STRONG COVER-AVOIDANCE PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 499-506
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Finite groups which are products of pairwise totally permutable subgroups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 41 / Issue 3 / October 1998
- Published online by Cambridge University Press:
- 20 January 2009, pp. 567-572
-
- Article
-
- You have access
- Export citation
A NOTE ON FINITE GROUPS GENERATED BY THEIR SUBNORMAL SUBGROUPS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 44 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 20 January 2009, pp. 417-423
-
- Article
-
- You have access
- Export citation



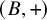
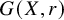
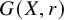
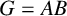
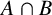
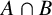
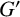
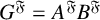
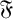
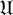
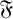
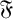
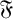
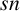
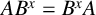
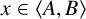
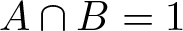
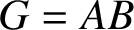
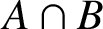
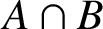
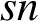
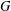
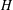
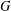

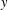
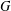
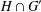

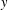
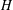
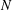
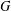
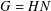
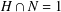
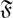
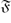
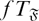
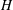
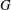
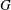
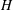
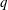
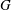
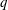
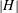
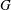
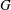
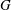
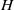
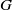
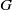

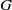
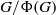
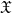
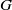
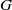
 -residual,
-residual, 