Article contents
ON A CLASS OF SUPERSOLUBLE GROUPS
Published online by Cambridge University Press: 23 May 2014
Abstract
A subgroup 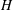 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}H$ of a finite group
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}H$ of a finite group 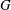 $G$ is said to be S-semipermutable in
$G$ is said to be S-semipermutable in 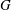 $G$ if
$G$ if 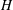 $H$ permutes with every Sylow
$H$ permutes with every Sylow 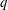 $q$-subgroup of
$q$-subgroup of 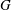 $G$ for all primes
$G$ for all primes 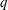 $q$ not dividing
$q$ not dividing 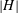 $|H |$. A finite group
$|H |$. A finite group 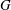 $G$ is an MS-group if the maximal subgroups of all the Sylow subgroups of
$G$ is an MS-group if the maximal subgroups of all the Sylow subgroups of 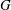 $G$ are S-semipermutable in
$G$ are S-semipermutable in 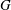 $G$. The aim of the present paper is to characterise the finite MS-groups.
$G$. The aim of the present paper is to characterise the finite MS-groups.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 90 , Issue 2 , October 2014 , pp. 220 - 226
- Copyright
- Copyright © 2014 Australian Mathematical Publishing Association Inc.
References
- 5
- Cited by


