Research Article
A determinant formula for a class of rational solutions of Painlevé V equation
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-25
-
- Article
-
- You have access
- Export citation
Boundary behavior of the Bergman metric
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 27-40
-
- Article
-
- You have access
- Export citation
On Gorenstein surfaces dominated by P2
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 41-63
-
- Article
-
- You have access
- Export citation
Shellability of semigroup rings
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 65-84
-
- Article
-
- You have access
- Export citation
Monogenesis of the rings of integers in certain imaginary abelian fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 85-92
-
- Article
-
- You have access
- Export citation
Numerical criteria for certain fiber spaces to be birationally trivial
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 93-103
-
- Article
-
- You have access
- Export citation
On the cohomological completeness of q-complete domains with corners
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 105-112
-
- Article
-
- You have access
- Export citation
The moduli space of bilevel-6 abelian surfaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 113-125
-
- Article
-
- You have access
- Export citation
Special rays in the Mori cone of a projective variety
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 127-137
-
- Article
-
- You have access
- Export citation
Glauber dynamics for fermion point processes
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 139-166
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 168 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f3
-
- Article
-
- You have access
- Export citation



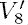 ). We can completely classify all such quotients. Some natural conjectures when the surface is not Gorenstein are also stated.
). We can completely classify all such quotients. Some natural conjectures when the surface is not Gorenstein are also stated.