Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-19T13:16:51.269Z Has data issue: false hasContentIssue false
  • English
  • Français

On Gorenstein surfaces dominated by P2

Published online by Cambridge University Press:  22 January 2016

R. V. Gurjar ,
C. R. Pradeep  and
D.-Q. Zhang
R. V. Gurjar
Affiliation:
School of Mathematics, Tata Institute of Fundamental research, Homi-Bhabha road, Mumbai 400005, India, gurjar@math.tifr.res.in
C. R. Pradeep
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore, 560012, India, pradeep@math.iisc.ernet.in
D.-Q. Zhang
Affiliation:
Department of Mathematics, National University of Singapore, 2 Science Drive 2, Singapore 117543, matzdq@math.nus.edu.sg
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we prove that a normal Gorenstein surface dominated by P2 is isomorphic to a quotient P2/G, where G is a finite group of automorphisms of P2 (except possibly for one surface 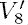). We can completely classify all such quotients. Some natural conjectures when the surface is not Gorenstein are also stated.

Keywords

14J2514J2614J45
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 168 , 2002 , pp. 41 - 63
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2002

References

[1] Alekseev, V. A. and Kolpakov-Miroshnichenko, I. Ya., On quotient surfaces of P2 by a finite group, Russian Math. Surveys, 43-5 (1988), 207–208.Google Scholar
[2] Bredon, G. E., Introduction to Compact Transformation Groups, Pure and Applied Mathematics, Vol. 46, Academic Press, 1972.Google Scholar
[3] Demazure, M., Surfaces de del Pezzo, Lecture Notes in Math. Vol. 777, Springer, Berlin-Heidelberg-New York, 1980.Google Scholar
[4] Hidaka, F. and Watanabe, K., Normal Gorenstein surfaces with ample anti-canonical divisor, Tokyo J. Math., 4 (1981), 319–330.Google Scholar
[5] Gurjar, R. V. and Shastri, A. R., The fundamental group at infinity of affine surfaces, Comment. Math. Helvitici, 59 (1984), 459–484.Google Scholar
[6] Mohan Kumar, N., Rational double points on a rational surface, Invent. Math., 65 (1981/82), 251–268.Google Scholar
[7] Lazarsfeld, R., Some applications of the theory of positive vector bundles, Complete intersections, Acireale, Lecture Notes in Mathematics, Vol. 1092 (1983), 29–61, Springer Verlag.Google Scholar
[8] Miyanishi, M., Normal Affine Subalgebras of a Polynomial Ring, Algebraic and Topo-logical Theories – to the memory of T. Miyata, 37-51, Kinokuniya, Tokyo, (1985).Google Scholar
[9] Miyanishi, M. and Zhang, D.-Q., Gorenstein log del Pezzo surfaces of rank one, Algebra J., 118 (1988), 63–84.CrossRefGoogle Scholar
[10] Mumford, D., The topology of normal singularities of an algebraic surface and a criterion for simplicity, Publ. Math. IHES, 9 (1961), 5–22.Google Scholar
[11] Seshadri, C. S., Quotient spaces modulo reductive algebraic groups, Ann. Math., 97 (1972), 511–556.Google Scholar
[12] Samuel, P., On Unique Factorization Domains, Tata Institute of Fundamental Research, Lectures on Mathematics and Physics, No. 30.Google Scholar