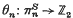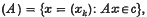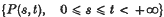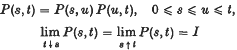Research Article
Periodic groups generated by finite amalgams
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 189-197
-
- Article
- Export citation
The geometric realization of Wall obstructions by nilpotent and simple spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 199-206
-
- Article
- Export citation
On certain non-trivial ribbon knots
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 207-211
-
- Article
- Export citation
Multiple points of codimension one immersions of oriented manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 213-220
-
- Article
- Export citation
Continuity properties of k-plane integrals and Besicovitch sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 221-226
-
- Article
- Export citation
Analytic functions having distributional boundary values in W′-spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 227-242
-
- Article
- Export citation
Generalized Nörlund means and consistency theorems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 243-248
-
- Article
- Export citation
Integrals with a large parameter: a double complex integral with four nearly coincident saddle-points
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 249-273
-
- Article
- Export citation
Applications of multiparameter spectral theory to special functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 275-283
-
- Article
- Export citation
The embedding problem for Markov chains with three states
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 285-294
-
- Article
- Export citation
Hamiltonian and algebro-geometric integrals of stationary equations of KdV type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 295-305
-
- Article
- Export citation
Qualitative analysis of a model for boundary effects in the Taylor problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-337
-
- Article
- Export citation
Bifurcations at a spherical hole in an infinite elastoplastic medium
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 339-356
-
- Article
- Export citation
Bifurcation of rotating circular cylindrical elastic membranes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-376
-
- Article
- Export citation
Front matter
PSP volume 87 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 87 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

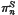 with the bordism group of oriented compact closed smooth
with the bordism group of oriented compact closed smooth