Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-26T10:35:47.818Z Has data issue: false hasContentIssue false
  • English
  • Français

Hamiltonian and algebro-geometric integrals of stationary equations of KdV type

Published online by Cambridge University Press:  24 October 2008

George Wilson
George Wilson
Affiliation:
Mathematical Institute, Oxford
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we shall generalize a theorem of Bogoyavl'enskii (2) showing the equivalence of two apparently different families of integrals of the ‘higher stationary Korteweg–de Vries (KdV)’ equations. We recall that the KdV equations form a hierarchy of evolution equations

for an unknown function u(x, t). The equations can be written in ‘Lax form’ (7)

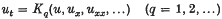
where L is the Schrödinger operator (δ2/δx2) + u, and P+ runs through all the (ordinary) differential operators such that the commutator on the right of (1·1) has order zero.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 87 , Issue 2 , March 1980 , pp. 295 - 305
Copyright
Copyright © Cambridge Philosophical Society 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Adler, M.On a trace functional for formal pseudo-differential operators and the symplectic structure of the Korteweg–de Vries equations. Invent. Math. 50 (1979), 219–248.CrossRefGoogle Scholar
(2)Bogoyavl'enskii, O. I.On integrals of higher stationary KdV equations and the eigenvalues of Hill's operator. Functional Anal. Appl. 10 (1976), 9–12 (Russian), 92–95 (English).Google Scholar
(3)Burchnall, J. L. and Chaundy, T. W.Commutative ordinary differential operators. Proc. London Math. Soc. 21 (1922), 420–440.Google Scholar
(4)Gel'fand, I. M. and Dikii, L. A.Fractional powers of operators and Hamiltonian systems. Functional Anal. Appl. 10 (1976), 13–29 (Russian), 259–273 (English).Google Scholar
(5)Gel'fand, I. M. and Dikii, L. A.Integrable non-linear equations and Liouville's theorem. Functional Anal. Appl. 13 (1979), 8–20 (Russian).Google Scholar
(6)Krichever, I. M.Integration of non-linear equations by the methods of algebraic geometry Functional Anal. Appl. 11 (1977), 15–31 (Russian), 12–26 (English).CrossRefGoogle Scholar
(7)Lax, P. D.Integrals of non-linear equations of evolution and solitary waves. Comm. Pure Appl. Math. 21 (1968), 467–490.CrossRefGoogle Scholar
(8)Lax, P. D.Periodic solutions of the KdV equation. Comm. Pure Appl. Math. 28 (1975), 141–188.Google Scholar
(9)Manin, Yu. I.Algebraic aspects of non-linear differential equations. Itogi Nauki i Tekhniki, ser. Sovremennye Problemy Matematiki 11 (1978), 5–152 (Russian); English Translation in J. Sov. Math. 11:1 (1979), 1–122.Google Scholar
(10)Novikov, S. P.The periodic problem for the Korteweg -de Vries equation. Functional Anal. Appl. 8 (1974), 54–66 (Russian), 236–246 (English).Google Scholar
(11)Veselov, A. P.On the Hamiltonian formalism for the Novikov–Krichever equations of commutativity of two operators. Functional Anal. Appl. 13 (1979), 1–7 (Russian).Google Scholar
(12)Wilson, G.Commuting flows and conservation laws for Lax equations. Math. Proc. Cambridge Philos. Soc. 86 (1979), 131–143.Google Scholar