This journal utilises an Online Peer Review Service (OPRS) for submissions. By clicking "Continue" you will be taken to our partner site https://cup.msp.org/submit/gmj. Please be aware that your Cambridge account is not valid for this OPRS and registration is required. We strongly advise you to read all "Author instructions" in the "Journal information" area prior to submitting.
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
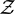 ${\mathcal{Z}}$-STABLE PROJECTIONLESS C*-ALGEBRAS
${\mathcal{Z}}$-STABLE PROJECTIONLESS C*-ALGEBRAS