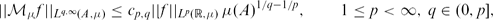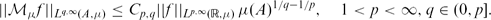Research Article
ON SS-SUPPLEMENTED SUBGROUPS OF FINITE GROUPS AND THEIR PROPERTIES
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 481-491
-
- Article
-
- You have access
- Export citation
WEYL TYPE THEOREMS FOR FUNCTIONS OF OPERATORS
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 493-505
-
- Article
-
- You have access
- Export citation
DOUBLES OF KLEIN SURFACES
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 507-515
-
- Article
-
- You have access
- Export citation
ON THE WILLMORE FUNCTIONAL OF 2-TORI IN SOME PRODUCT RIEMANNIAN MANIFOLDS
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 517-528
-
- Article
-
- You have access
- Export citation
GROUPS THAT INVOLVE FINITELY MANY PRIMES AND HAVE ALL SUBGROUPS SUBNORMAL II
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 529-534
-
- Article
-
- You have access
- Export citation
EXISTENCE OF INFINITELY MANY SOLUTIONS FOR SUBLINEAR ELLIPTIC PROBLEMS
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 535-545
-
- Article
-
- You have access
- Export citation
ON THE DOUBLE TRANSFER AND THE f-INVARIANT
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 547-577
-
- Article
-
- You have access
- Export citation
PARA-BLASCHKE ISOPARAMETRIC HYPERSURFACES IN A UNIT SPHERE Sn + 1(1)*
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 579-597
-
- Article
-
- You have access
- Export citation
ON KELLOGG'S THEOREM FOR QUASICONFORMAL MAPPINGS
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 599-603
-
- Article
-
- You have access
- Export citation
RINGS WHOSE CYCLIC MODULES ARE DIRECT SUMS OF EXTENDING MODULES
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 605-617
-
- Article
-
- You have access
- Export citation
THE HOMOTOPY TYPE OF THE SPACE OF GRADIENT VECTOR FIELDS ON THE TWO-DIMENSIONAL DISC
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 619-626
-
- Article
-
- You have access
- Export citation
ANOTHER LAW FOR 3-METABELIAN GROUPS
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 627-628
-
- Article
-
- You have access
- Export citation
ON THE GEOMETRY OF ORBIT CLOSURES FOR REPRESENTATION-INFINITE ALGEBRAS
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 629-636
-
- Article
-
- You have access
- Export citation
A NEW QUANTITY IN RIEMANN-FINSLER GEOMETRY*
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 637-645
-
- Article
-
- You have access
- Export citation
A NOETHER–DEURING THEOREM FOR DERIVED CATEGORIES
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 647-654
-
- Article
-
- You have access
- Export citation
BEST CONSTANTS IN THE WEAK-TYPE ESTIMATES FOR UNCENTERED MAXIMAL OPERATORS
-
- Published online by Cambridge University Press:
- 30 March 2012, pp. 655-663
-
- Article
-
- You have access
- Export citation
(n + 1)-TENSOR NORMS OF LAPRESTÉ'S TYPE
-
- Published online by Cambridge University Press:
- 31 July 2012, pp. 665-692
-
- Article
-
- You have access
- Export citation
SUBGROUPS OF FINITE INDEX IN (2, 3, n)-TRIANGLE GROUPS
-
- Published online by Cambridge University Press:
- 31 July 2012, pp. 693-714
-
- Article
-
- You have access
- Export citation
AN ALGEBRAIC-METRIC EQUIVALENCE RELATION OVER p-ADIC FIELDS
-
- Published online by Cambridge University Press:
- 31 July 2012, pp. 715-720
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
GMJ volume 54 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 31 July 2012, pp. f1-f2
-
- Article
-
- You have access
- Export citation




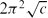 .
.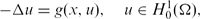
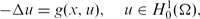 for all
for all