Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-07-02T21:25:49.306Z Has data issue: false hasContentIssue false
  • English
  • Français

BEST CONSTANTS IN THE WEAK-TYPE ESTIMATES FOR UNCENTERED MAXIMAL OPERATORS

Published online by Cambridge University Press:  30 March 2012

ADAM OSȨKOWSKI
ADAM OSȨKOWSKI*
Affiliation:
Faculty of Mathematics, Informatics and Mechanics, University of Warsaw, Banacha 2, 02-097 Warsaw, Poland e-mail: ados@mimuw.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let μ be a Borel measure on ℝ. The paper contains the proofs of the estimates 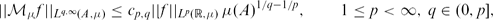and 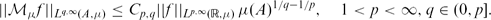Here A is a subset of ℝ, f is a μ-locally integrable function, 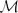μ is the uncentred maximal operator with respect to μ and cp,q, and Cp,q are finite constants depending only on the parameters indicated. In the case when μ is the Lebesgue measure, the optimal choices for cp,q and Cp,q are determined. As an application, we present some related tight bounds for the strong maximal operator on ℝn with respect to a general product measure.

Keywords

Primary: 42B25Secondary: 42B3546E30
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 54 , Issue 3 , September 2012 , pp. 655 - 663
Copyright
Copyright © Glasgow Mathematical Journal Trust 2012

References

REFERENCES

1.Bernal, A., A note on the one-dimensional maximal function, Proc. Roy. Soc. Edinburgh 111A (1989), 325–328.CrossRefGoogle Scholar
2.Grafakos, L. and Kinnunen, J., Sharp inequalities for maximal functions associated with general measures, Proc. Roy. Soc. Edinburgh 128A (1998), 717–723.CrossRefGoogle Scholar
3.Grafakos, L. and Montgomery-Smith, S., Best constants for uncentered maximal functions, Bull. London Math. Soc. 29 (1997), 60–64.CrossRefGoogle Scholar
4.Hardy, G. H., Littlewood, J. E. and Pólya, G., Inequalities, 2nd ed. (Cambridge University Press, Cambridge, UK, 1952).Google Scholar
5.Sjögren, P., A remark on the maximal function for measures in ℝn, Amer. J. Math. 105 (1983), 1231–1233.CrossRefGoogle Scholar
6.Stein, E. M., Harmonic analysis: Real variable theory, orthogonality, and oscillatory integrals (Princeton University Press, Princeton, NJ, 1993).Google Scholar