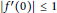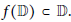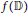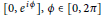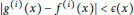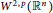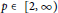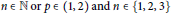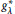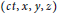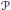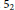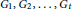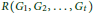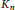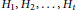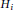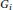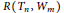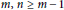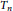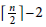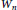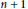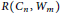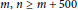Research Article
The Contraction Principle for Multivalued Mappings on a Modular Metric Space with a Graph
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-12
-
- Article
-
- You have access
- Export citation
On Classes
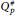 for Hyperbolic Riemann Surfaces
for Hyperbolic Riemann Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 13-29
-
- Article
-
- You have access
- Export citation
A Geometric Extension of Schwarz’s Lemma and Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 30-35
-
- Article
-
- You have access
- Export citation
Distributive and Anti-distributive Mendelsohn Triple Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 36-49
-
- Article
-
- You have access
- Export citation
On the Bernstein Problem in the Three-dimensional Heisenberg Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 50-61
-
- Article
-
- You have access
- Export citation
Uncertainty Principles on Weighted Spheres, Balls, and Simplexes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 62-72
-
- Article
-
- You have access
- Export citation
Positive Solutions for the Generalized Nonlinear Logistic Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 73-86
-
- Article
-
- You have access
- Export citation
Approximation of a Function and its Derivatives by Entire Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 87-94
-
- Article
-
- You have access
- Export citation
Faithful Representations of Graph Algebras via Branching Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 95-103
-
- Article
-
- You have access
- Export citation
Littlewood–Paley Characterizations of Second-Order Sobolev Spaces via Averages on Balls
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 104-118
-
- Article
-
- You have access
- Export citation
A Simple Proof and Strengthening of a Uniqueness Theorem for L-functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 119-122
-
- Article
-
- You have access
- Export citation
Discrete Space-time and Lorentz Transformations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 123-135
-
- Article
-
- You have access
- Export citation
Transformation Formulas for Bilinear Sums of Basic Hypergeometric Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 136-143
-
- Article
-
- You have access
- Export citation
A Brief Note Concerning Hard Lefschetz for Chow Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 144-158
-
- Article
-
- You have access
- Export citation
Rotors in Khovanov Homology
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 159-169
-
- Article
-
- You have access
- Export citation
A Note on Fine Graphs and Homological Isoperimetric Inequalities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 170-181
-
- Article
-
- You have access
- Export citation
Generalized Torsion in Knot Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 182-189
-
- Article
-
- You have access
- Export citation
Ramsey Number of Wheels Versus Cycles and Trees
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 190-196
-
- Article
-
- You have access
- Export citation
Quasi-copure Submodules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 197-203
-
- Article
-
- You have access
- Export citation
Restricted Khinchine Inequality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 204-210
-
- Article
-
- You have access
- Export citation



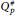 for Hyperbolic Riemann Surfaces
for Hyperbolic Riemann Surfaces