Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-23T13:03:50.538Z Has data issue: false hasContentIssue false
  • English
  • Français

A Geometric Extension of Schwarz’s Lemma and Applications

Published online by Cambridge University Press:  20 November 2018

Galatia Cleanthous
Galatia Cleanthous*
Affiliation:
Department of Mathematics, Aristotle University of Thessaloniki, Thessaloniki 54124, Greece e-mail: gkleanth@math.auth.gr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

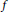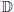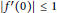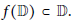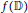Let $f$ be a holomorphic function of the unit disc $\mathbb{D}$ , preserving the origin. According to Schwarz’s Lemma, $\left| {{f}^{\prime }}(0) \right|\,\le \,1$ , provided that $f(\mathbb{D})\,\subset \,\mathbb{D}$ . We prove that this bound still holds, assuming only that $f(\mathbb{D})$ does not contain any closed rectilinear segment 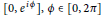$\left[ 0,\,{{e}^{i\phi }} \right],\,\phi \,\in \,\left[ 0,\,2\pi \right]$ , i.e., does not contain any entire radius of the closed unit disc. Furthermore, we apply this result to the hyperbolic density and give a covering theorem.

Keywords

30C8030C2530C99Schwarz’s Lemmapolarizationhyperbolic densitycovering theorems
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 1 , 01 March 2016 , pp. 30 - 35
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Beardon, A. F. and Minda, D., The hyperbolic metric and geometric function theory. In: Quasiconformal mappings and their applications, Narosa Publishing House, New Delhi, India, 2007, pp. 9–56.Google Scholar
[2] Betsakos, D., Geometric versions of Schwarz's lemma for quasiregular mappings. Proc. Amer. Math. Soc. 139(2011), 1397–1407. http://dx.doi.Org/10.1090/S0002-9939-2010-10604-4 Google Scholar
[3] Bermant, A., On certain generalizations of E. Lindelof's principle and their applications. Mat. Sb. 20(62)(1947), 55–112.Google Scholar
[4] Burckel, R. B., Marshall, D. E., Minda, D., Poggi-Corradini, P., and Ransford, T. J., Area, capacity and diameter versions of Schwarz's lemma. Conform. Geom. Dyn. 12(2008), 133–152. http://dx.doi.Org/10.1090/S1088-4173-08-00181-1 Google Scholar
[5] Cleanthous, G., Monotonicity theorems for analytic functions centered at infinity. Proc. Amer. Math. Soc. 142(2014), 3545–3551. http://dx.doi.Org/10.1090/S0002-9939-2014-12084-3 Google Scholar
[6] Cleanthous, G. and Georgiadis, A. G., Multi-point bounds for analytic functions under measure conditions. Complex Var. Elliptic Equ. 60(2015), 470–477. http://dx.doi.Org/10.1080/17476933.2014.944864 Google Scholar
[7] Dubinin, V. N., Symmetrization in the geometric theory of functions of a complex variable. (Russian) Uspekhi Math. Nauk. 49(1994), 3–76; translation in Russian Math. Surveys 49(1994), 1-79. http://dx.doi.Org/10.1070/RM1994v049n01ABEH002002 Google Scholar
[8] Dubinin, V. N., Geometric versions of Schwarz's lemma and symmetrization. J. Math. Sci. (N. Y.) 178(2011), 150–157.Google Scholar
[9] Hayman, W. K. and Kennedy, P. B., Subharmonic functions. Vol. I., London Mathematical Society Monographs, 9, Academic Press, London-New York, 1976.Google Scholar
[10] Hayman, W. K., Subharmonic functions. Vol. IL, London Mathematical Society Monographs, 20, Ademic Press, London, 1989.Google Scholar
[11] Hayman, W. K., Multivalent functions. Second éd., Cambridge Tracts in Mathematics, 110, Cambridge University Press, Cambridge, 1994. http://dx.doi.Org/10.1017/CBO9780511526268 Google Scholar
[12] Nevanlinna, R., Analytic functions. Springer-Verlag, New York-Berlin, 1970.Google Scholar
[13] Solynin, A.Yu., Polarization and functional inequalities. Algebra i Analiz 8(1996), 148–185 (Russian); English translation in St. Petersburg Math. J. 8(1997), 1015-1038.Google Scholar
[14] Solynin, A.Yu., A Schwarz lemma for meromorphic functions and estimates for the hyperbolic metric. Proc. Amer. Math. Soc. 136(2008), 3133–3143. http://dx.doi.Org/10.1090/S0002-9939-08-09309-X Google Scholar