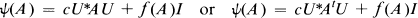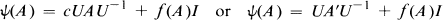Research Article
Tubes, Cohomology with Growth Conditions and an Application to the Theta Correspondence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-37
-
- Article
-
- You have access
- Export citation
N Subspaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 38-54
-
- Article
-
- You have access
- Export citation
Generalized Variation and Functions of Slow Growth
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 55-85
-
- Article
-
- You have access
- Export citation
An Index Theory for Semigroups of *-Endomorphisms of
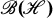 and Type II1 Factors.
and Type II1 Factors.
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 86-114
-
- Article
-
- You have access
- Export citation
Inequalities in Discrete Subgroups of PSL(2, R)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 115-130
-
- Article
-
- You have access
- Export citation
Higher Derivations and Distinguished Subfields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 131-141
-
- Article
-
- You have access
- Export citation
The MOD 2 K-Homology of Ω3S3X
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 142-196
-
- Article
-
- You have access
- Export citation
K-Theory and Asymptotically Commuting Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 197-216
-
- Article
-
- You have access
- Export citation
Shape Equivalences of Whitney Continua of Curves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 217-227
-
- Article
-
- You have access
- Export citation
A Tauberian Theorem Concerning Borel-Type and Cesàro Methods of Summability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 228-247
-
- Article
-
- You have access
- Export citation
Commutativity Preserving Maps of Factors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 248-256
-
- Article
-
- You have access
- Export citation



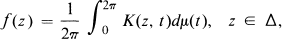
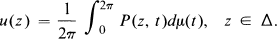
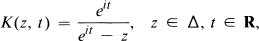
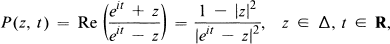
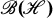 and Type II
and Type II and type II
and type II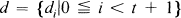
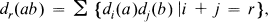
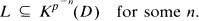
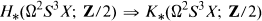
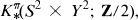
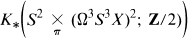
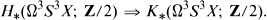
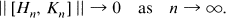
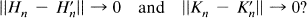
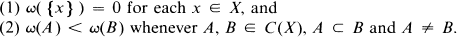
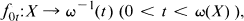
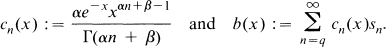
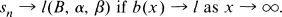
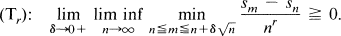
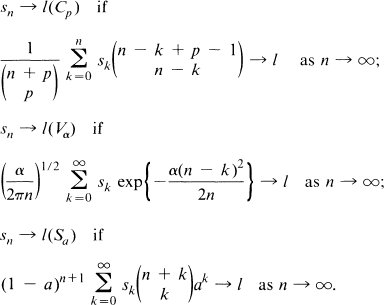
 which contains
which contains 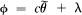 where
where 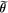 is an isomorphism or an antiisomorphism,
is an isomorphism or an antiisomorphism,