Article contents
The MOD 2 K-Homology of Ω3S3X
Published online by Cambridge University Press: 20 November 2018
Extract
In order to compute the group K*(Ω3S3X; Z/2) when X is a finite, torsion free CW-complex we apply the techniques developed by Snaith in [38], [39], [40], [41] which were used in [42] to determine the Atiyah-Hirzebruch spectral sequence ( [11], [1, Part III])
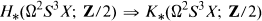
for X as above. Roughly speaking the method consists in defining certain classes in K*(Ω3S3X; Z/2) via the π-equivariant mod 2 K-homology of S2 × Y2,
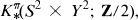
([35]), π the cyclic group of order 2 (acting antipodally on S2, by permuting factors in Y2, and diagonally on S2 × Y2), Y a finite subcomplex of Ω3S3X, and then showing that the classes so produced map under the edge homomorphism to cycles (in the E1-term of the Atiyah-Hirzebruch spectral sequence for
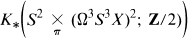
which determine certain homology classes of H*(Ω3S3X; Z/2), thus exhibiting these as infinite cycles of the spectral sequence
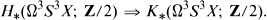
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1988
References
- 1
- Cited by


