Article contents
Commutativity Preserving Maps of Factors
Published online by Cambridge University Press: 20 November 2018
Extract
By a von Neumann algebra M we mean a weakly closed, self-adjoint algebra of operators on a Hilbert space 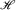 which contains I, the identity operator. A factor is a von Neumann algebra whose centre consists of scalar multiples of I.
which contains I, the identity operator. A factor is a von Neumann algebra whose centre consists of scalar multiples of I.
In all that follows ϕ:M → N will be a one to one, *-linear map from the von Neumann factor M onto the von Neumann algebra N such that both ϕ and ϕ−1 preserve commutativity. Our main result states that if M is not of type I2 then 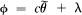 where
where 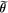 is an isomorphism or an antiisomorphism, c is a non-zero scalar, and λ is a *-linear map from M into ZN, the centre of N.
is an isomorphism or an antiisomorphism, c is a non-zero scalar, and λ is a *-linear map from M into ZN, the centre of N.
Our interest in this problem was aroused by several recent results. In [1], Choi, Jafarian, and Radjavi proved that if S is the real linear space of n × n matrices over any algebraically closed field, n ≧ 3, and ψ a linear operator on S which preserves commuting pairs of matrices, then either ψ(S) is commutative or there exists a unitary matrix U such that
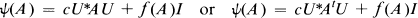
for all A in S. They proved an analogous result for the collection of all bounded self-adjoint operators on an infinite dimensional Hilbert space when ψ is one to one. Subsequently, Omladic [7] proved that if ψ:L(X) → L(X) is a bijective linear operator preserving commuting pairs of operators where X is a non-trivial Banach space, then
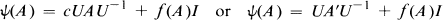
where U is a bounded invertible operator on X and A′ is the adjoint of A.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1988
References
- 14
- Cited by


